
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| BE |
| e1 |
| e2 |
| EC |
| e1 |
| e2 |
| e1 |
| e2 |
| BC |
| AE |
| AB |
| BE |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| AE |
| EC |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
|
| 1 |
| 2 |
| 3 |
| 2 |
| BC |
| BE |
| EC |
| e1 |
| 1 |
| 2 |
| e2 |
| AD |
| BC |
| AD |
| BC |
|
|


科目:高中数学 来源: 题型:
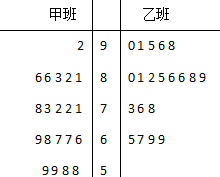 我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.
我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com