练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系xOy中，曲线C1的参数方程为（α为参数），直线C2的方程为，以O为极点，x轴的正半轴为极轴建立极坐标系．

    （1）求曲线C1和直线C2的极坐标方程；

    （2）若直线C2与曲线C1交于A，B两点，求．

    【答案】（1）极坐标方程为，（2） .

    【解析】

    试题（1）根据极坐标和直角坐标的互化公式得极坐标方程为ρ2﹣4ρcosθ﹣4ρsinθ+7=0

    直线C2的方程为y= ，极坐标方程为 ；（2）直线C2与曲线C1联立，可得ρ2﹣（2+2 ）ρ+7=0，

    （1）曲线C1的参数方程为 （α为参数），直角坐标方程为（x﹣2）2+（y﹣2）2=1，即x2+y2﹣4x﹣4y+7=0，极坐标方程为ρ2﹣4ρcosθ﹣4ρsinθ+7=0

    直线C2的方程为y= ，极坐标方程为 ；

    （2）直线C2与曲线C1联立，可得ρ2﹣（2+2 ）ρ+7=0，

    设A，B两点对应的极径分别为ρ1，ρ2，则ρ1+ρ2=2+2，ρ1ρ2=7， ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图是一个高为4长方体截去一个角所得的多面体的直观图及它的正（主）视图和侧（左）视图（单位：）

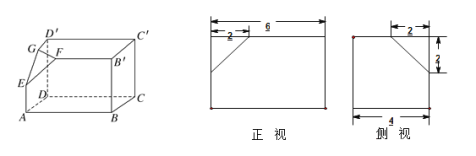
    （1）求异面直线与所成角的余弦；

    （2）将求异面直线与所成的角转化为求一个三角形的内角即可，要求只写出找角过程，不需计算结果；

    （3）求异面直线与所成的角；要求同（2）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2＋2aln x.

    (1)当a＝1时，求函数f′(x)的最小值；

    (2)求函数f(x)的单调区间和极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）证明：当时，函数在上是单调函数；

    （2）当时，恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给定函数①;②;③；④，其中在区间上单调递减的函数序号是( )

    A.①②B.②③C.③④D.①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】4支足球队进行单循环比赛（任两支球队恰进行一场比赛），任两支球队之间胜率都是．单循环比赛结束，以获胜的场次数作为该队的成绩，成绩按从大到小排名次顺序，成绩相同则名次相同．下列结论中正确的是（ ）

    A.恰有四支球队并列第一名为不可能事件B.有可能出现恰有三支球队并列第一名

    C.恰有两支球队并列第一名的概率为D.只有一支球队名列第一名的概率为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，的内切圆于边、、分别切于点、、，、、、的中点分别为、、、，与交于点。证明：的外接圆与的内切圆相切。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某科技公司新研制生产一种特殊疫苗，为确保疫苗质量，定期进行质量检验．某次检验中，从产品中随机抽取100件作为样本，测量产品质量体系中某项指标值，根据测量结果得到如下频率分布直方图：

    (1)求频率分布直方图中的值；

    (2)技术分析人员认为，本次测量的该产品的质量指标值X服从正态分布，若同组中的每个数据用该组区间的中间值代替，计算，并计算测量数据落在(187.8，212.2)内的概率；

    (3)设生产成本为y元，质量指标值为，生产成本与质量指标值之间满足函数关系假设同组中的每个数据用该组区间的中间值代替，试计算生产该疫苗的平均成本．

    参考数据：,．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知五边形ABECD由一个直角梯形和一个等边三角形构成（如图1所示），且．将梯形沿着折起（如图2所示），点是的中点，平面

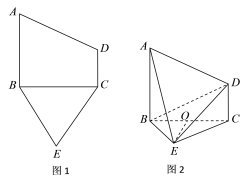
    （1）求证：；

    （2）若，求二面角的余弦值．

    查看答案和解析>>

    同步练习册答案