
分析 (1)由动圆M恒过F(1,0)且与直线x=-1相切得,点M到F(1,0)与到直线x=-1距离相等,结合抛物线定义可得圆心M的轨迹C的方程;联立直线方程与抛物线方程,化为关于x的一元二次方程,由判别式大于0求得直线l的斜率k的取值范围;
(2)设D(x0,y0),A(x1,y1),B(x2,y2),写出DA、DB的方程,求出与x=1的交点P、Q的坐标,可得$\overrightarrow{OP}•\overrightarrow{OQ}$,结合根与系数的关系及D在抛物线上求得$\overrightarrow{OP}•\overrightarrow{OQ}$的值;
(3)联立$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=k(x+\frac{p}{2})}\end{array}\right.$ 得,k2x2+(pk2-2p)x$+\frac{{{k^2}{p^2}}}{4}=0$.然后与(2)同法求解$\overrightarrow{OP}•\overrightarrow{OQ}$的值.
解答 (1)解:由动圆M恒过F(1,0)且与直线x=-1相切得,点M到F(1,0)与到直线x=-1距离相等,
∴圆心M的轨迹C的方程为:y2=4x;
联立$\left\{\begin{array}{l}{y^2}=4x\\ y=k({x+1})\end{array}\right.$得,k2x2+(2k2-4)x+k2=0,
∴$\left\{\begin{array}{l}{x_1}+{x_2}=-({2{k^2}-4})\\{x_1}{x_2}=1\end{array}\right.$,
当k=0时,一次方程只有一个根,不成立;
∴$\left\{\begin{array}{l}k≠0\\△>0\end{array}\right.$,即$\left\{\begin{array}{l}{k≠0}\\{(2{k}^{2}-4)^{2}-4{k}^{4}>0}\end{array}\right.$,解得k∈(-1,0)∪(0,1).
∴直线l的斜率k的取值范围为k∈(-1,0)∪(0,1);
(2)证明:设D(x0,y0),A(x1,y1),B(x2,y2),
直线lDA:$y-{y_0}=\frac{4}{{{y_0}+{y_1}}}({x-{x_0}})$,即lDA:(y0+y1)y=4x+y0y1
其与x=1的交点$P({1,\frac{{{y_0}{y_1}+4}}{{{y_0}+{y_1}}}})$,
同理lDB与x=1的交点$Q({1,\frac{{{y_0}{y_2}+4}}{{{y_0}+{y_2}}}})$,
∴$\overrightarrow{OP}•\overrightarrow{OQ}=1+$$({\frac{{{y_0}{y_1}+4}}{{{y_0}+{y_1}}}})•({\frac{{{y_0}{y_2}+4}}{{{y_0}+{y_2}}}})=1+$$\frac{{y_0^2{y_1}{y_2}+4{y_0}({{y_1}+{y_2}})+16}}{{y_0^2+{y_0}({{y_1}+{y_2}})+{y_1}{y_2}}}$.
由(1)中的x1x2=1得,${y_1}{y_2}=\sqrt{16{x_1}{x_2}}=4$,代入上式得$\frac{{4y_0^2+4{y_0}({{y_1}+{y_2}})+16}}{{y_0^2+{y_0}({{y_1}+{y_2}})+4}}=4$.
故$\overrightarrow{OP}•\overrightarrow{OQ}$=1+4=5;
(3)解:联立$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=k(x+\frac{p}{2})}\end{array}\right.$ 得,k2x2+(pk2-2p)x$+\frac{{{k^2}{p^2}}}{4}=0$.
∴${x_1}{x_2}=\frac{p^2}{4}$,得${y_1}{y_2}=\sqrt{4{p^2}{x_1}{x_2}}$=p2,
直线lDA:$y-{y_0}=\frac{2p}{{{y_0}+{y_1}}}({x-{x_0}})$,即lDA:(y0+y1)y=2px+y0y1,
得$P({\frac{p}{2},\frac{{{y_0}{y_1}+{p^2}}}{{{y_0}+{y_1}}}})$,$Q({\frac{p}{2},\frac{{{y_0}{y_2}+{p^2}}}{{{y_0}+{y_2}}}})$.
∴$\overrightarrow{OP}•\overrightarrow{OQ}=\frac{p^2}{4}+$$\frac{{y_0^2{y_1}{y_2}+{p^2}{y_0}({{y_1}+{y_2}})+{p^2}}}{{y_0^2+{y_0}({{y_1}+{y_2}})+{y_1}{y_2}}}$=$\frac{p^2}{4}+{p^2}=\frac{{5{p^2}}}{4}$,$\overrightarrow{OP}•\overrightarrow{OQ}=\frac{{5{p^2}}}{4}$.
点评 本题考查直线与抛物线位置关系的,训练了向量法在求解圆锥曲线问题中的应用,考查计算能力,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [1,+∞) | C. | (-∞,0) | D. | (-∞,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x^2}$ | B. | y=lg10x | C. | $y=\frac{x^2}{x}$ | D. | $y={(\sqrt{x-1})^2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
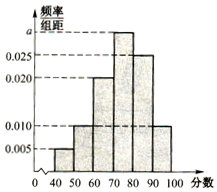 为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com