
分析 (1)极坐标方程两边同乘ρ,根据极坐标与直角坐标的对于关系得出直角坐标方程;
(2)把直线l的参数方程代入曲线C的方程,利用根与系数的关系和参数的几何意义化简即可得出结论.
解答 解:(1)∵ρ-ρcos2θ-4cosθ=0,∴ρ2-ρ2cos2θ-4ρcosθ=0,
∴x2+y2-x2-4x=0,即y2=4x.
(2)把为$\left\{\begin{array}{l}x=a+tcosθ\\ y=tsinθ\end{array}\right.(t$为参数,θ为倾斜角)代入y2=4x得:
sin2θ•t2-4cosθ•t-4a=0,
∴t1+t2=$\frac{4cosθ}{si{n}^{2}θ}$,t1t2=-$\frac{4a}{si{n}^{2}θ}$,
∴$\frac{1}{{{{|{QA}|}^2}}}+\frac{1}{{{{|{QB}|}^2}}}$=$\frac{1}{{{t}_{1}}^{2}}+\frac{1}{{{t}_{2}}^{2}}$=$\frac{{{t}_{1}}^{2}+{{t}_{2}}^{2}}{{{t}_{1}}^{2}{{t}_{2}}^{2}}$=$\frac{({t}_{1}+{t}_{2})^{2}-2{t}_{1}{t}_{2}}{{{t}_{1}}^{2}{{t}_{2}}^{2}}$=$\frac{16co{s}^{2}θ+8asi{n}^{2}θ}{16{a}^{2}}$,
∴当a=2时,$\frac{1}{{{{|{QA}|}^2}}}+\frac{1}{{{{|{QB}|}^2}}}$为定值$\frac{1}{4}$.
点评 本题考查了参数方程的几何意义,极坐标与直角坐标的转化,属于中档题.


科目:高中数学 来源: 题型:解答题
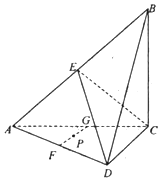 如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.
如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
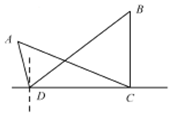 如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.
如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
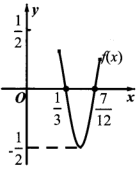 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | $(-\frac{1}{24}+2kπ,\frac{5}{24}+2kπ)$,(k∈Z) | B. | $(-\frac{1}{12}+\frac{k}{2},\frac{5}{12}+\frac{k}{2})$,(k∈Z) | ||
| C. | $(-\frac{1}{12}+2kπ,\frac{1}{3}+2kπ)$,(k∈Z) | D. | $(-\frac{1}{24}+\frac{k}{2},\frac{5}{24}+\frac{k}{2})$,(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
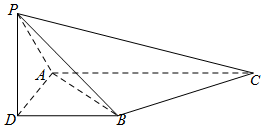 如图,三棱锥P-ABC,侧棱PA=2,底面三角形ABC为正三角形,边长为2,顶点P在平面ABC上的射影为D,有AD⊥DB,且DB=1.
如图,三棱锥P-ABC,侧棱PA=2,底面三角形ABC为正三角形,边长为2,顶点P在平面ABC上的射影为D,有AD⊥DB,且DB=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com