
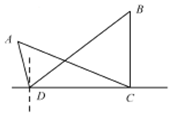
 如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.
如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里. 分析 分别在△ACD和△BCD中利用正弦定理计算AD,BD,再在△ABD中利用余弦定理计算AB.
解答 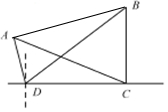 解:连接AB,
解:连接AB,
由题意可知CD=40,∠ADC=105°,∠BDC=45°,∠BCD=90°,∠ACD=30°,
∴∠CAD=45°,∠ADB=60°,
在△ACD中,由正弦定理得$\frac{AD}{sin30°}=\frac{40}{sin45°}$,∴AD=20$\sqrt{2}$,
在Rt△BCD中,
∵∠BDC=45°,∠BCD=90°,
∴BD=$\sqrt{2}$CD=40$\sqrt{2}$.
在△ABD中,由余弦定理得AB=$\sqrt{800+3200-2×20\sqrt{2}×40\sqrt{2}×cos60°}$=20$\sqrt{6}$.
故答案为:$20\sqrt{6}$.
点评 本题考查了解三角形的应用,合理选择三角形,利用正余弦定理计算是关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 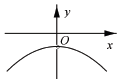 | B. | 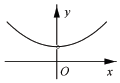 | C. | 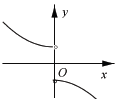 | D. | 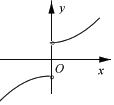 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2} | C. | {-2,1,2} | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}-4$ | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com