
分析 命题p:方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{m-5}$=1表示双曲线,(m-2)(m-5)<0,解得m范围.命题q:x∈(0,+∞),x2-mx+4≥0恒成立,则m≤x+$\frac{4}{x}$的最小值,利用基本不等式的性质即可得出.若p∨q是真命题,且?(p∧q)也是真命题,(即(p∧q)是假命题),p与q必然一真一假.进而得出.
解答 解:命题p:方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{m-5}$=1表示双曲线,(m-2)(m-5)<0,解得2<m<5.
命题q:x∈(0,+∞),x2-mx+4≥0恒成立,则m≤x+$\frac{4}{x}$的最小值,
∵x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,当且仅当x=2时取等号.∴m≤4.
若p∨q是真命题,且?(p∧q)也是真命题,(即(p∧q)是假命题),
∴p与q必然一真一假.
∴$\left\{\begin{array}{l}{2<m<5}\\{m>4}\end{array}\right.$,或$\left\{\begin{array}{l}{m≤2或m≥5}\\{m≤4}\end{array}\right.$,
解得4<m<5,或m≤2.
∴m的取值范围是(-∞,2]∪(4,5).
点评 本题考查了简易逻辑的判定方法、基本不等式的性质、双曲线的标准方程、,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 35种 | B. | 70种 | C. | 210种 | D. | 105种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:
如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
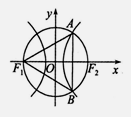 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22016-1 | B. | 3•21008-3 | C. | 22009-3 | D. | 22010-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为5.
《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com