Question

7．已知S是边长为a的等边三角形ABC所在平面外一点，SA=SB=SC，D为AB的中点，且SD与BC所成的角为45°，求SD与平面ABC所成角的正弦值．

Answer 1

分析 取AC的中点E，连接DE，SE，则DE∥BC，可得∠SDE=45°，求出SD=$\frac{\sqrt{2}}{4}$a，S在三角形ABC中的射影为三角形ABC的中心O，再求出SO，即可求出SD与平面ABC所成角的正弦值．

解答 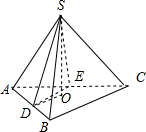解：取AC的中点E，连接DE，SE，则DE∥BC，
∵SD与BC所成的角为45°，
∴∠SDE=45°，
∵SD=SE，
∴DE=$\sqrt{2}$SD，
∴SD=$\frac{\sqrt{2}}{4}$a，
∵S是边长为a的等边三角形ABC所在平面外一点，SA=SB=SC，
∴S在三角形ABC中的射影为三角形ABC的中心O，
∵OD=$\frac{\sqrt{3}}{6}$a，
∴SO=$\frac{\sqrt{6}}{12}$a，
∴SD与平面ABC所成角的正弦值为$\frac{\frac{\sqrt{6}}{12}a}{\frac{\sqrt{2}}{4}a}$=$\frac{\sqrt{3}}{3}$．

点评 本题考查线面角，考查学生的计算能力，属于中档题．