
分析 先根据题意可表示出过焦点的直线与双曲线方程联立求得交点M的坐标,F1,F2的坐标,进而表示出$\overrightarrow{M{F}_{1}}$,$\overrightarrow{M{F}_{2}}$,进而根据cos∠F1MF2=0,即$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,求得a和b的关系,进而求得a和c的关系,离心率可得.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,F2(c,0),
依题意$\left\{\begin{array}{l}{{b}^{2}{x}^{2}-{a}^{2}{y}^{2}={a}^{2}{b}^{2}}\\{y=\frac{b}{a}(x-c)}\end{array}\right.$,解得x=$\frac{{a}^{2}+{c}^{2}}{2c}$,y=-$\frac{{b}^{3}}{2ac}$,
即有M($\frac{{a}^{2}+{c}^{2}}{2c}$,-$\frac{{b}^{3}}{2ac}$),F1(-c,0),F2(c,0),
∴$\overrightarrow{M{F}_{1}}$=($\frac{-{a}^{2}-3{c}^{2}}{2c}$,$\frac{{b}^{3}}{2ac}$),$\overrightarrow{M{F}_{2}}$=($\frac{{b}^{2}}{2c}$,$\frac{{b}^{3}}{2ac}$),
∵cos∠F1MF2=0,即有$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,
即$\frac{-{a}^{2}-3{c}^{2}}{2c}$•$\frac{{b}^{2}}{2c}$+$\frac{{b}^{3}}{2ac}$•$\frac{{b}^{3}}{2ac}$=0,
∴c4=5a2c2,
∴e=$\frac{c}{a}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题主要考查了双曲线的简单性质,考查了学生综合分析问题和解决问题的能力.圆锥曲线是高考的重点每年必考,希望能够引起考生的重视.


科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{1}{5}$] | B. | [-$\frac{1}{3}$,1] | C. | (-∞,-$\frac{1}{3}$]∪[$\frac{1}{5}$,+∞) | D. | (-∞,-$\frac{1}{3}$]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于( )
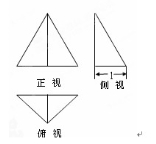
A.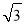 B.
B.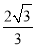 C.
C.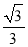 D.
D.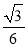
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com