练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】格纸中每个正方形的边长为1，粗线部分是一个几何体的三视图，则该几何体最长棱的棱长是

    A. 3 B. 6 C. D. 5

    【答案】D

    【解析】画出立体图（如图）．由图知，该几何体最长棱的棱长是5．

    点睛:三视图问题的常见类型及解题策略

    (1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．

    (2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．

    (3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．

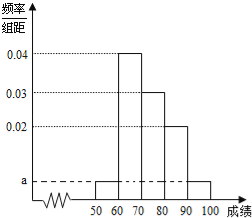
    （1）求图中a的值；

    （2）根据频率分布直方图，估计这100名学生语文成绩的平均分；

    （3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“杨辉三角”又称“贾宪三角”，是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算，而杨辉在公元1261年所著的《详解九章算法》一书中，记录了贾宪三角形数表，并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数是（ ）

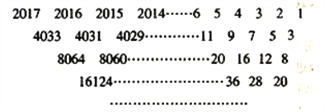
    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年5月13日第30届大连国际马拉松赛举行，某单位的10名跑友报名参加了半程马拉松、10公里健身跑、迷你马拉松3个项目(每人只报一项)，报名情况如下：

    项目

    半程马拉松

    10公里健身跑

    迷你马拉松

    人数

    2

    3

    5

    (其中：半程马拉松公里，迷你马拉松公里)

    (1)从10人中选出2人，求选出的两人赛程距离之差大于10公里的概率；

    (2)从10人中选出2人，设为选出的两人赛程距离之和，求随机变量的分布列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题：
    ·（1）y=|cos（2x+ ）|最小正周期为π；
    ·（2）函数y=tan 的图象的对称中心是（kπ，0），k∈Z；
    ·（3）f（x）=tanx﹣sinx在（﹣ ， ）上有3个零点；
    ·（4）若 ∥ ， ，则
    其中错误的是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知．

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）若函数在上有最小值，且最小值为，满足，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数

    （1）当时，求函数的单调区间；

    （2）令，其图象上任意一点处切线的斜率恒成立，求实数的取值范围.

    （3）当时，方程在区间内有唯一实数解，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

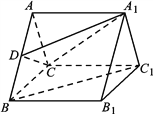
    【题目】如图，在三棱柱中，底面△ABC是等边三角形，侧面为正方形，且平面ABC， 为线段上的一点．

    (Ⅰ) 若∥平面A1CD，确定D的位置，并说明理由；

    (Ⅱ) 在(Ⅰ)的条件下，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3+x2+mx在x=1处有极小值，

    g（x）=f（x）﹣x3﹣x2+x﹣alnx．

    （1）求函数f（x）的单调区间；

    （2）是否存在实数a，对任意的x1、x2∈（0，+∞），且x1≠x2，有恒成立？若存在，求出a的取值范围；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案