
一个非空集合中的各个元素之和是3的倍数,则称该集合为“好集”.
记集合 {1,2,3,…,3n}的子集中所有“好集”的个数为f(n).
(1)求f(1),f(2)的值;
(2)求f(n)的表达式.
(1)易得f(1)=3;
当n=2时,集合{1,2,3,4,5,6}的子集中是“好集”的有:
单元集:{3},{6}共2个,双元集{1,2},{1,5},{2,4},{4,5},{3,6}共5个,三元集有:{1,2,3},{1,2,6},{1,3,5},{1,5,6},{4,2,3},{4,2,6},{4,3,5},{4,5,6}共8个,四元集有{3,4,5,6},{2,3,4,6},{1,3,5,6},{1,2,3,6},{1,2,4 ,5}共五个,五元集{1,2,4,5,6},{1,2,3,4,5}共2个,还有一个全集.
故f(2)=1+(2+5)×2+8=23.
(2)首先考虑f(n+1)与f(n)的关系.
集合{1,2,3,…,3n,3n+1,3n+2,3n+3}在集合{1,2,3,…,3n}中加入3个元素3n+1,3n+2,3n+3.故f(n+1)的组成有以下几部分:①原还的f(n)个集合;②含有元素3n+1的“好集”是{1,2,3,…,3n}中各元素之和被3除余2的集合,含有元素是3n+2的“好集”是{1,2,3,…,3n}中各元素之和被3除余1的集合,含有元素是3n+,3的“好集”是{1,2,3,…,3n}中各元素之和被3除余0的集合,合计是23n;③含有元素是3n+1与3n+2的“好集”是{1,2,3,…,3n}中各元素之和被3除余0的集合,含有元素是3n+2与3n+3的“好集”是{1,2,3,…,3n}中各元素之和被3除余1的集合,含有元素是3n+1与3n+3的“好集”是{1,2,3,…,3n}中各元素之和被3除余2的集合,合计是23n;④含有元素是3n+1,3n+2,3n+3的“好集”是{1,2,3,…,3n}中“好集”与它的并,再加上{3n+1,3n+2,3n+3}。
所以,f(n+1)=2 f(n)+2×23n+1.
两边同除以2n+1,得 -
-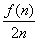 =4n+
=4n+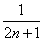 ,
,
所以 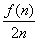 =4n-1+4n-2+…+4+
=4n-1+4n-2+…+4+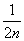 +
+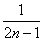 +…+
+…+ +
+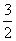 =
=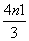 +1-
+1-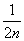 ,
,
即f(n)=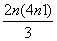 +2n-1.
+2n-1.


科目:高中数学 来源: 题型:
已知点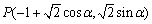 (其中
(其中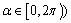 ,点
,点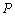 的轨迹记为曲线
的轨迹记为曲线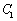 ,以坐标原点为极点,
,以坐标原点为极点,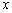 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点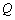 在曲线
在曲线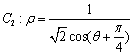 上.
上.
(Ⅰ)求曲线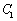 的极坐标方程和曲线
的极坐标方程和曲线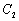 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当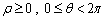 时,求曲线
时,求曲线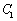 与曲线
与曲线 的公共点的极坐标.
的公共点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
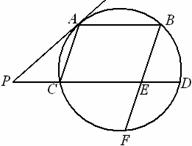
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.
查看答案和解析>>
科目:高中数学 来源: 题型:
假设在6分钟内的任意时刻,两架相同型号的飞机机会均等地进入同一飞机场,若这两架飞机进入机场的时间之差不小于2分钟,飞机不会受到干扰;则飞机受到干扰的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
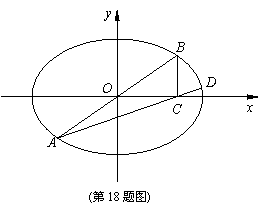
在平面直角坐标系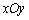 中,已知椭圆
中,已知椭圆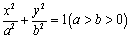 与直线
与直线 相交于
相交于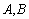 两点(从左至右),过点
两点(从左至右),过点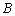 作
作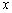 轴的垂线,垂足为
轴的垂线,垂足为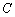 ,直线
,直线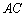 交椭圆于另一点
交椭圆于另一点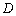 .
.
(1)若椭圆的离心率为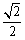 ,点
,点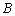 的坐标为
的坐标为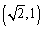 ,求椭圆的方程;
,求椭圆的方程;
 (2)若以
(2)若以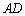 为直径的圆恰好经过点
为直径的圆恰好经过点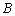 ,求椭圆的离心率.
,求椭圆的离心率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com