
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ,0).
,0).
(1)求双曲线C的方程;
(2)若直线l:y=kx+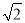 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且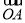 ·
· >2(其中O为原点),求k的取值范围.
>2(其中O为原点),求k的取值范围.
(1)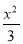 -y2=1
-y2=1
(2)(-1,-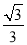 )∪(
)∪(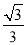 ,1)
,1)
【解析】(1)设双曲线C的方程为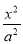 -
-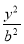 =1(a>0,b>0).
=1(a>0,b>0).
由已知得a= ,c=2,再由c2=a2+b2得b2=1,
,c=2,再由c2=a2+b2得b2=1,
所以双曲线C的方程为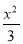 -y2=1.
-y2=1.
(2)将y=kx+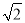 代入
代入 -y2=1中,整理得(1-3k2)x2-6
-y2=1中,整理得(1-3k2)x2-6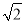 kx-9=0,
kx-9=0,
由题意得
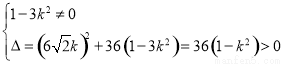 ,
,
故k2≠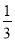 且k2<1 ①.
且k2<1 ①.
设A(xA,yA),B(xB,yB),则xA+xB=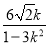 ,xAxB=
,xAxB=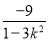 ,
,
由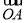 ·
·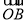 >2得xAxB+yAyB>2,
>2得xAxB+yAyB>2,
xAxB+yAyB=xAxB+(kxA+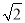 )(kxB+
)(kxB+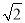 )=(k2+1)xAxB+
)=(k2+1)xAxB+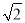 k(xA+xB)+2=(k2+1)·
k(xA+xB)+2=(k2+1)·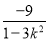 +
+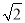 k·
k·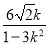 +2=
+2= ,
,
于是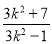 >2,即
>2,即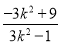 >0,解得
>0,解得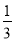 <k2<3 ②.
<k2<3 ②.
由①②得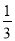 <k2<1,
<k2<1,
所以k的取值范围为(-1,-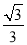 )∪(
)∪(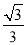 ,1).
,1).


科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:填空题
某班有48名学生,在一次考试中统计出平均分为70,方差为75,后来发现有2名同学的分数登记错了,甲实际得80分却记成了50分,乙实际得70分却记成了100分,更正后平均分为________,方差为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:填空题
若过点P(1,1)且互相垂直的两条直线l1,l2分别与x轴,y轴交于A,B两点,则AB中点M的轨迹方程为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:选择题
如图,F为抛物线y2=4x的焦点,A,B,C在抛物线上,若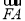 +
+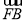 +
+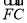 =0,则|
=0,则|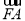 |+|
|+|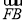 |+|
|+|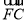 |=( )
|=( )
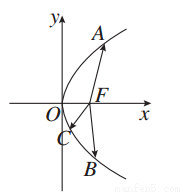
A.6 B.4 C.3 D.2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:选择题
对于抛物线y2=4x上任意一点Q,点P(a,0)满足|PQ|≥|a|,则a的取值范围是( )
A.(-∞,0) B.(-∞,2] C.[0,2] D.(0,2)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-6双曲线(解析版) 题型:解答题
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为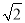 ,且过点(4,-
,且过点(4,- ).
).
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证: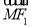 ·
·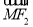 =0;
=0;
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-6双曲线(解析版) 题型:选择题
双曲线x2+my2=1的虚轴长是实轴长的2倍,则双曲线的渐近线方程为( )
A.y=±2x B.y=±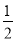 x C.y=±
x C.y=±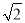 x D.y=±
x D.y=±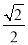 x
x
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
A. B.
B. C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:填空题
若两平行直线3x-2y-1=0,6x+ay+c=0之间的距离为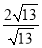 ,则
,则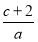 的值为________.
的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com