练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．${C}_{2014}^{0}$•20+${C}_{2014}^{2}$•22+…+${C}_{2014}^{2014}$•22014=$\frac{{3}^{2014}+1}{2}$．

    分析 根据二项式的展开式，利用赋值法，进行适当的变形，即可求出代数式的值．

    解答 解：由（1+x）2014=${C}_{2014}^{0}$•x0+${C}_{2014}^{1}$•x1+${C}_{2014}^{2}$•x2+${C}_{2014}^{3}$•x3+…+${C}_{2014}^{2013}$•x2013+${C}_{2014}^{2014}$•x2014，
    令x=2，得
    （1+2）2014=${C}_{2014}^{0}$•20+${C}_{2014}^{1}$•21+${C}_{2014}^{2}$•22+${C}_{2014}^{3}$•23+…+${C}_{2014}^{2013}$•22013+${C}_{2014}^{2014}$•22014，
    令x=-2，得
    （1-2）2014=${C}_{2014}^{0}$•20-${C}_{2014}^{1}$•21+${C}_{2014}^{2}$•22-${C}_{2014}^{3}$•23+…-${C}_{2014}^{2013}$•22013+${C}_{2014}^{2014}$•22014，
    以上两式相加得
    ${C}_{2014}^{0}$•20+${C}_{2014}^{2}$•22+…+${C}_{2014}^{2014}$•22014=$\frac{{3}^{2014}+1}{2}$．
    故答案为：$\frac{{3}^{2014}+1}{2}$．

    点评 本题考查了利用二项式的展开式，把自变量进行适当的赋值，从而计算代数式值的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．数列{an}前n项和Sn=2n，则a3+a4=12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知集合A={x|x2-x-6＞0），B={x|-1≤x≤4），则A∩B=（　　）
    A．[-l，3）B．（3，4]C．[-1，2）D．（2，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．某学校共有3125名学生，一次活动中全体学生被排成一个n排的等腰梯形阵，且这n排学生数按每排都比前一排
    多一人的规律排列，则当n取到最大值时，排在这等腰梯形阵最外面的一周的学生总人数是（　　）
    A．296B．221C．225D．641

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

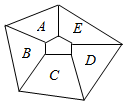    13．如图，在A，B，C，D，E五个区域中栽种3种植物，要求同一区域中只种1种植物，相邻两区域所种植物不同，则不同的栽种方法的总数为（　　）
    A．21B．24C．30D．48

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．数轴上有2个点A、B，最初A在原点，B在坐标2的位置．规定如下，若投掷出来的硬币为正面，则A点坐标加上1，B点坐标不动；反之，若投掷出来的硬币是反面，则B点坐标加上1，A点坐标不动．求下列事件发生的概率
    （1）硬币投4次，A的坐标为3的概率；
    （2）A比B先到坐标4的概率；
    （3）硬币投掷6次，A第一次追上B的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知曲线$y=\frac{1}{3}{x^3}+\frac{4}{3}$．
    （1）求曲线过点P（2，4）的切线方程；
    （2）求满足斜率为1的曲线的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数f（x）=2sin2（ωx+$\frac{π}{6}$）（ω＞0）在区间[$\frac{π}{6}$，$\frac{2π}{3}$]内单调递增，则ω的最大值是（　　）
    A．$\frac{3}{4}$B．$\frac{3}{5}$C．$\frac{1}{2}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知不等式9ax+8≥$\frac{36x}{2{x}^{2}+1}$+1在[$\frac{1}{2}$，+∞）上恒成立，则实数a的取值范围是（　　）
    A．（$\frac{8}{9}$，+∞）B．（-∞，$\frac{8}{9}$）C．[$\frac{8}{9}$，+∞）D．（-∞，$\frac{8}{9}$]

    查看答案和解析>>

    同步练习册答案