
| A. | $\frac{{{e^2}-2e-1}}{4e}$ | B. | $\frac{{{e^2}-2e}}{4e}$ | C. | $\frac{{{e^2}-e-1}}{4e}$ | D. | $\frac{{{e^2}-1}}{4e}$ |
分析 首先画出图形,利用定积分求出阴影部分面积,然后利用面积比求概率.
解答 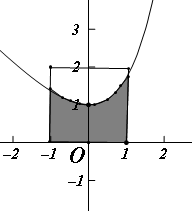 解:由题意y=ex-x的图象以及不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$所确定的区域为E如图:
解:由题意y=ex-x的图象以及不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$所确定的区域为E如图:
区域E的面积为边长为2 的正方形的面积为4,
在此范围内区域D的面积为${∫}_{-1}^{1}({e}^{x}-x)dx=({e}^{x}-\frac{1}{2}{x}^{2}){|}_{-1}^{1}=e-\frac{1}{e}$,
由几何概型的公式得到所求概率为$\frac{e-\frac{1}{e}}{4}=\frac{{e}^{2}-1}{4e}$;
故选:D.
点评 本题主要考查线性规划的基本应用,利用z的几何意义是解决线性规划问题的关键,注意利用数形结合来解决.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
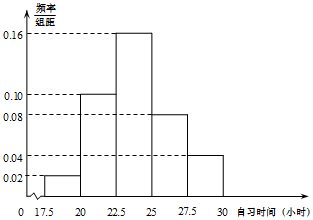 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )| A. | 30 | B. | 60 | C. | 80 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 10 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
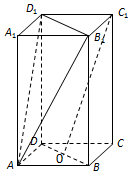 如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.
如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com