练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．设等差数列{an}的前n项和为Sn，若a4，a6是方程x2-18x+p=0的两根，那么S9=（　　）
    A．9B．81C．5D．45

    分析 利用韦达定理求出a4+a6=18，再由等差数列通项公式和前n项和公式得S9=$\frac{9}{2}（{a}_{1}+{a}_{9}）$=$\frac{9}{2}$（a4+a6），由此能求出结果．

    解答 解：∵等差数列{an}的前n项和为Sn，
    a4，a6是方程x2-18x+p=0的两根，那
    ∴a4+a6=18，
    ∴S9=$\frac{9}{2}（{a}_{1}+{a}_{9}）$=$\frac{9}{2}（{a}_{4}+{a}_{6}）=\frac{9}{2}×18$=81．
    故选：B．

    点评 本题考查等差数列的前9项和的求法，涉及到韦达定理、等差数列等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．狄利克雷函数是高等数学中的一个典型函数，若f（x）=$\left\{\begin{array}{l}{1，x∈Q}\\{0，x∈{C}_{R}Q}\end{array}\right.$，则称f（x）为狄利克雷函数．对于狄利克雷函数f（x），给出下面4个命题：①对任意x∈R，都有f[f（x）]=1；②对任意x∈R，都有f（-x）+f（x）=0；③对任意x1∈R，都有x2∈Q，f（x1+x2 ）=f（x1）；④对任意a，b∈（-∞，0），都有{x|f（x）＞a}={x|f（x）＞b}．其中所有真命题的序号是（　　）
    A．①④B．③④C．①②③D．①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

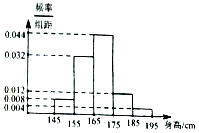    20．某校共有学生1800人，现从中随机抽取一个50人的样本，以估计该校学生的身体状况，测得样本身高小于195cm的频率分布直方图如图，由此估计该校身高不小于175的人数是288．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设f（x）=x2+ax+2（a∈R），若{y|y=f（f（x））}={y|y=f（x）}，则实数a的取值范围是（-∞，-2]∪[4，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知$a={log_2}3，b={2^{-\frac{1}{3}}}，c={log_{\frac{1}{3}}}\frac{1}{30}$，则a、b、c的大小关系是（　　）
    A．c＞a＞bB．a＞c＞bC．a＞b＞cD．c＞b＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．用“五点法”画y=2sin（2x+$\frac{π}{3}$）在一个周期内的简图时，所描的五个点分别是（$-\frac{π}{6}$，0），（$\frac{π}{12}$，2），（$\frac{π}{3}$，0），（$\frac{7π}{12}$，-2），（$\frac{5π}{6}$，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．把8个相同的小球全部放入编号为1，2，3，4的四个盒中，则不同的放法数为（　　）
    A．35B．70C．165D．1860

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设曲线y=ex-x及直线y=0所围成的图形为区域D，不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$所确定的区域为E，在区域E内随机取一点，则该点落在区域D内的概率为（　　）
    A．$\frac{{{e^2}-2e-1}}{4e}$B．$\frac{{{e^2}-2e}}{4e}$C．$\frac{{{e^2}-e-1}}{4e}$D．$\frac{{{e^2}-1}}{4e}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．某人午觉醒来，发现表停了，他打开收音机，想听电台报时，则他等待时间大于10分钟的概率为（　　）
    A．$\frac{1}{6}$B．$\frac{5}{6}$C．$\frac{1}{10}$D．$\frac{9}{10}$

    查看答案和解析>>

    同步练习册答案