
分析 (1)利用三种方程的转化方法,写出直线l的普通方程和曲线C1的参数方程;
(2)设点$P({cosθ,\sqrt{3}sinθ})$,点P到直线l的距离$d=\frac{{|{\sqrt{3}cosθ-\sqrt{3}sinθ+2\sqrt{3}}|}}{{\sqrt{3+1}}}=\frac{{\sqrt{3}|{\sqrt{2}sin({θ-\frac{π}{4}})-2}|}}{2}$,即可求点P到直线l距离的最小值.
解答 解:(1)直线l的普通方程为$\sqrt{3}x-y+2\sqrt{3}=0$,曲线C1的参数方程为$\left\{\begin{array}{l}x=\sqrt{6}cosθ\\ y=\sqrt{6}sinθ\end{array}\right.(θ$为参数).
(2)由题意知,曲线C2的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=\sqrt{3}sinθ\end{array}\right.(θ$为参数),
可设点$P({cosθ,\sqrt{3}sinθ})$,
故点P到直线l的距离为$d=\frac{{|{\sqrt{3}cosθ-\sqrt{3}sinθ+2\sqrt{3}}|}}{{\sqrt{3+1}}}=\frac{{\sqrt{3}|{\sqrt{2}sin({θ-\frac{π}{4}})-2}|}}{2}$,
所以${d_{min}}=\frac{{2\sqrt{3}-\sqrt{6}}}{2}$,即点P到直线l的距离的最小值为$\frac{{2\sqrt{3}-\sqrt{6}}}{2}$.
点评 本题考查三种方程的转化,考查参数方程的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
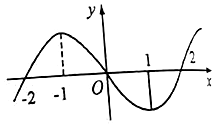 已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )
已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )| A. | (-2,0)∪(2,+∞) | B. | (-∞,2)∪(2,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-2,-1)∪(1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 66 | B. | 55 | C. | 44 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 5 | 9 | 10 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 14 | 10 | 6 | 4 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 4 | 8 | 16 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | 6 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
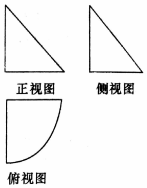 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )| A. | 2 | B. | π+4 | C. | $\sqrt{2}π+4$ | D. | $({\sqrt{2}+1})π+4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
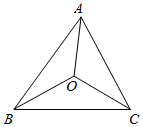 如图,已知O为△ABC的外心,角A、B、C的对边分别为a、b、c.
如图,已知O为△ABC的外心,角A、B、C的对边分别为a、b、c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com