
���� ��1�����ö����ظ�����ĸ��ʹ�ʽ���ס������ҹ�˾�����2����Ŀ�ĸ��ʣ�
��2�����˾��ȷ������Ե�����ΪX����X��ȡֵ�ֱ�Ϊ1��2��3��������ʣ��õ�X�ķֲ�������������ҹ�˾��ȷ������Ե���ΪY����Yȡֵ�ֱ�Ϊ0��1��2��3��������ʵõ��ֲ��У�����������ɣ�
��� �⣺��1���������֪���������$P=\frac{C_4^1C_2^2}{C_6^3}��C_3^1{��{\frac{2}{3}}��^1}{��{1-\frac{2}{3}}��^2}+\frac{C_4^2C_2^1}{C_6^3}��{��{1-\frac{2}{2}}��^3}=\frac{1}{15}$��
��2�����˾��ȷ������Ե�����ΪX����X��ȡֵ�ֱ�Ϊ1��2��3.$P��{X=1}��=\frac{C_4^1C_2^2}{C_6^3}=\frac{1}{5}$��$P��X=2��=\frac{C_4^2C_2^1}{C_6^3}=\frac{3}{5}$��$P��{X=3}��=\frac{C_4^3C_2^0}{C_6^3}=\frac{1}{5}$��
��X�ķֲ���Ϊ��
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
| Y | 0 | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{2}{9}$ | $\frac{4}{9}$ | $\frac{8}{27}$ |
���� ���⿼������ظ���������Լ��ֲ������������������������


 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x+3��2+��y-1��2=1 | B�� | ��x-3��2+��y+1��2=1 | C�� | ��x+3��2+��y+1��2=1 | D�� | ��x-3��2+��y-1��2=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{13}}}{3}$ | B�� | $\frac{{2\sqrt{13}}}{3}$ | C�� | $\frac{{\sqrt{13}}}{5}$ | D�� | $\frac{{2\sqrt{13}}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
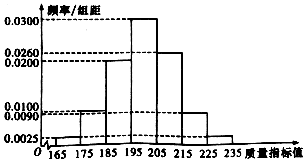 ij�ֲ�Ʒ��������������ָ�����������������ָ��ֵ���ֵȼ������
ij�ֲ�Ʒ��������������ָ�����������������ָ��ֵ���ֵȼ������| ����ָ��ֵm | m��185 | 185��m��205 | M��205 |
| �ȼ� | ����Ʒ | ����Ʒ | һ��Ʒ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2016}$ | B�� | $\frac{1}{2017}$ | C�� | $\frac{1}{2018}$ | D�� | $\frac{1}{2019}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com