
(本小题满分14分)已知等差数列 的前
的前 项和为
项和为 ,前
,前 项和为
项和为 .
.
1)求数列 的通项公式
的通项公式
2)设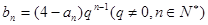 , 求数列
, 求数列 的前
的前 项和
项和 .
.
(1)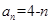 ;(2)Sn=
;(2)Sn=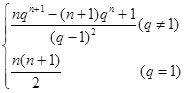 。
。
解析试题分析:(1)设{an}的公差为d ,由已知得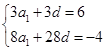
解得a1=3,d=-1
故an=3-(n-1)(-1)=4-n…………………………………………6分
(2)由(1)的解答得,bn=n·qn-1,于是
Sn=1·q0+2·q1+3·q2+……+(n-1)·qn-1+n·qn.
若q≠1,将上式两边同乘以q,得
qSn=1·q1+2·q2+3·q3+……+(n-1)·qn+n·qn+1.
将上面两式相减得到
(q-1)Sn=nqn-(1+q+q2+……+qn-1)
=nqn-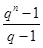
于是Sn=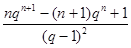
若q=1,则Sn=1+2+3+……+n=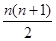
所以,Sn=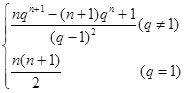 ……………………………………14分
……………………………………14分
考点:等差数列的性质;等差数列的通项公式;数列前n项和的求法。
点评:(1)若一个数列是等差数列和等比数列的乘积的形式,求其前n项和通常用错位相减法。(2)注意等比数列前n项和的形式: 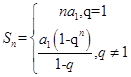 ,注意对
,注意对 的讨论。
的讨论。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本题满分16分)
已知数列 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为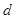 的等差数列;
的等差数列; 是公差为
是公差为 的等差数列(
的等差数列( ).
).
(Ⅰ)若 = 30,求
= 30,求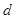 ;
;
(Ⅱ)试写出a30关于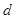 的关系式,并求a30的取值范围;
的关系式,并求a30的取值范围;
(Ⅲ)续写已知数列,可以使得 是公差为
是公差为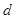 3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出
3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出 关于
关于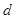 的关系式(
的关系式( N
N );
);
(Ⅳ)在(Ⅲ)条件下,且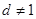 ,试用
,试用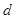 表示此数列的前100项和
表示此数列的前100项和
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列 中的
中的 、
、 、
、 .
.
(1)求数列 的通项公式; (2)数列
的通项公式; (2)数列 的前n项和为
的前n项和为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)
若S 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,且
的前n项和,且 成等比数列。
成等比数列。
(1)求等比数列 的公比;
的公比;
(2)若 ,求
,求 的通项公式;
的通项公式;
(3)在(2)的条件下,设 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
把正奇数数列 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
………………………
……………………………
设
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数.
个数.
(1)若 ,求
,求 的值;
的值;
(2)若记三角形数表中从上往下数第 行各数的和为
行各数的和为 ,求证
,求证 .(本题满分14分)
.(本题满分14分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com