
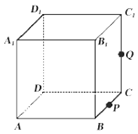
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. | A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 1对选项逐个进行检验即可,对于①:得到0<DT<1,可以容易得到S为四边形;对于②则找其投影即可;对于③,则需要找线面垂直关系即可;对于④,则需补图完成.
解答  解:设截面与DD1相交于T,则AT∥PQ,且AT=2PQ⇒DT=2CQ.
解:设截面与DD1相交于T,则AT∥PQ,且AT=2PQ⇒DT=2CQ.
对于①,当0<CQ<$\frac{1}{2}$时,则0<DT<1,所以截面S为四边形,且S为梯形,故①正确;
对于②,当CQ>$\frac{1}{2}$时,投影面积不为$\frac{3}{4}$,故②不正确;
对于③,存在某个位置,使得截面S与平面A1BD垂直,故③正确;
对于④,当CQ=$\frac{3}{4}$时,如图,
延长DD1至N,使D1N=$\frac{1}{2}$,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=$\frac{1}{3}$,故④正确;
故选:C.
点评 本题重点考查了空间几何体的结构特征、空间中点线面的位置关系等知识,考查命题真假的判断与应用,涉及正方体的截面问题,属中档题.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}-\frac{{4\sqrt{3}}}{9}$ | B. | $π-\frac{{4\sqrt{3}}}{9}$ | C. | $\frac{π}{2}+\frac{{4\sqrt{3}}}{9}$ | D. | $π+\frac{{4\sqrt{3}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.025 | B. | 0.050 | C. | 0.950 | D. | 0.975 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∧q为假命题,则p,q至少之一为假命题 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若am2<bm2,则a<b”的否命题是假命题 | |
| D. | “若$\overrightarrow a∥\overrightarrow c$且$\overrightarrow b∥\overrightarrow c$,则$\overrightarrow a∥\overrightarrow b$”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com