练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知a∈R，则“a＜3”是“|x+2|+|x-1|＞a恒成立”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 利用绝对值不等式的性质求出a的范围，结合充分条件和必要条件的定义是解决本题的关键．

    解答 解：∵|x+2|+|x-1≥|x+2-x+1|=3，
    ∴若|x+2|+|x-1|＞a恒成立，则a＜3，
    即“a＜3”是“|x+2|+|x-1|＞a恒成立”的充要条件，
    故选：C

    点评 本题主要考查充分条件和必要条件的判断，结合绝对值不等式的性质求出a的范围是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

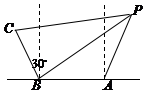    18．为捍卫钓鱼岛及其附属岛屿的领土主权，中国派出舰船“唐山号”、“石家庄号”和“邯郸号”在钓鱼岛领海巡航．某日，正巡逻在A处的“唐山号”突然发现来自P处的疑似敌舰的某信号，发现信号时“石家庄号”和“邯郸号”正分别位于如图所示的B、C两处，其中A在B的正东方向相距6海里处，C在B的北偏西30°方向相距4海里处．由于B、C比A距P更远，因此，4秒后B、C才同时发现这一信号（该信号的传播速度为每秒1海里），试确定疑似敌舰相对于A点“唐山号”的位置．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知复数z=$\frac{2+i}{1-2i}$，则$\overline{z}$=（　　）
    A．iB．-iC．1D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设命题p：?x∈（-∞，0），2x＜x2，则￢p为（　　）
    A．$?{x_0}∈[{0，+∞}），{2^{x_0}}≥{x_0}^2$B．$?{x_0}∈（{-∞，0}），{2^{x_0}}≥{x_0}^2$
    C．?x∈（-∞，0），2x≥x2D．?x∈[0，+∞），2x＜x2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若正实数x，y满足x2+2xy-1=0，则2x+y的最小值为$\sqrt{3}$ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．如图，由抛物线y2=8x与直线x+y-6=0及x轴所围成的图形（图中阴影部分）的面积为$\frac{40}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

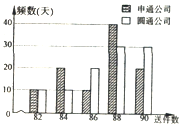    20．几年来，网上购物风靡，快递业迅猛发展，某市的快递业务主要由两家快递公司承接，即圆通公司与申通公司：“快递员”的工资是“底薪+送件提成”：这两家公司对“快递员”的日工资方案为：圆通公司规定快递员每天底薪为70元，每送件一次提成1元；申通公司规定快递员每天底薪为120元，每日前83件没有提成，超过83件部分每件提成10元，假设同一公司的快递员每天送件数相同，现从这两家公司各随机抽取一名快递员并记录其100天的送件数，得到如下条形图：
    （1）求申通公司的快递员一日工资y（单位：元）与送件数n的函数关系；
    （2）若将频率视为概率，回答下列问题：
    ①记圆通公司的“快递员”日工资为X（单位：元），求X的分布列和数学期望；
    ②小王想到这两家公司中的一家应聘“快递员”的工作，如果仅从日收入的角度考虑，请你利用所学过的统计学知识为他作出选择，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设a，b∈（0，+∞），则“a＞b”是“logab＜1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=sinxcosx+$\sqrt{3}$cos（π-x）cosx
    （Ⅰ）求f（x）的最小正周期；
    （Ⅱ）求f（x）在区间[0，$\frac{π}{2}$]上的最大值和最小值．

    查看答案和解析>>

    同步练习册答案