
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,a) | D. | (-∞,a] |
分析 分别求出x≤0时,x>0时,函数f(x)的值域,再由?x0∈[2,+∞)使得f(-x0)=f(x0),即为$\sqrt{{x}_{0}}$+a=(x0-1)3+1有解,运用参数分离和构造函数,求出导数,判断符号,可得单调性,即可得到f(x)的值域,再由不等式恒成立思想,可得b的范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{\sqrt{-x}+a,x≤0}\\{(x-1)^{3}+1,x>0}\end{array}$,
当x≤0时,f(x)=$\sqrt{-x}$+a≥a;
当x>0时,f(x)=(x-1)3+1递增,可得f(x)>0.
由?x0∈[2,+∞)使得f(-x0)=f(x0),
即为$\sqrt{{x}_{0}}$+a=(x0-1)3+1有解,
即为a=(x0-1)3+1-$\sqrt{{x}_{0}}$,
由y=(x0-1)3+1-$\sqrt{{x}_{0}}$,x0∈[2,+∞),
导数为3(x0-1)2-$\frac{1}{2\sqrt{{x}_{0}}}$>0在x0∈[2,+∞)恒成立,
即为函数y在x0∈[2,+∞)递增,
即有a≥2-$\sqrt{2}$>0,
则函数f(x)的值域为(0,+∞).
由任意的x∈R,f(x)>b恒成立,
可得b≤0.
故选:B.
点评 本题考查导数的运用:求单调性,考查分段函数的值域,注意运用单调性,考查不等式恒成立问题的解法,注意转化为求函数的值域,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直角梯形ABCD中,AB=2,CD=CB=1,∠ABC=90°,平面ABCD外有一点E,平面ADE⊥平面ABCD,AE=ED=1.
在直角梯形ABCD中,AB=2,CD=CB=1,∠ABC=90°,平面ABCD外有一点E,平面ADE⊥平面ABCD,AE=ED=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
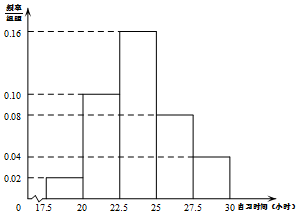 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )| A. | 26.25 | B. | 26.5 | C. | 26.75 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,0) | C. | (0,+∞) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com