
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 化简复数为a+bi的形式,即可判断对应点所在象限.
解答 解:设z=x+yi,
$\frac{2-3i}{3+2i}$+z=$\frac{(2-3i)^{2}}{(3+2i)(3-2i)}$+x+yi=$\frac{-5-12i}{13}$+x+yi=$\frac{-5}{13}$+x+(y-$\frac{12}{13}$)i,
∴x-$\frac{5}{13}$=2,y-$\frac{12}{13}$=-2,
∴x=$\frac{31}{13}$,y=-$\frac{14}{13}$,
∴z在复数平面内对应的点为($\frac{31}{13}$,-$\frac{14}{13}$),
故选:D.
点评 本题考查复数的代数形式的混合运算,复数的几何意义,基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{65}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1007 | B. | 1008 | C. | 1009.5 | D. | 1010 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,a) | D. | (-∞,a] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $3\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
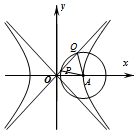 如图,已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$,且$|{\overrightarrow{OQ}}|=3|{\overrightarrow{OP}}$|,则双曲线C的离心率为( )
如图,已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$,且$|{\overrightarrow{OQ}}|=3|{\overrightarrow{OP}}$|,则双曲线C的离心率为( )| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{7}}}{4}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com