
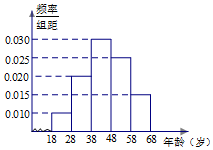
 ij��˾������Ϊ���������ܷ����ٰ취��֪ʶ�ʴ�������Ը���18��68�����Ⱥ��ȡһ������Ϊn�������������������ݷֳ����飺[18��28����[28��38����[38��48����[48��58����[58��68]���ٽ��䰴�����ҵ�˳��ֱ���Ϊ��1�飬��2�飬������5�飬������������Ƶ�ʷֲ�ֱ��ͼ�����Իش������������ͳ�ƺ�����±���ʾ��
ij��˾������Ϊ���������ܷ����ٰ취��֪ʶ�ʴ�������Ը���18��68�����Ⱥ��ȡһ������Ϊn�������������������ݷֳ����飺[18��28����[28��38����[38��48����[48��58����[58��68]���ٽ��䰴�����ҵ�˳��ֱ���Ϊ��1�飬��2�飬������5�飬������������Ƶ�ʷֲ�ֱ��ͼ�����Իش������������ͳ�ƺ�����±���ʾ��| ��� | ���� | �ش���ȷ������ | �ش���ȷ ������ռ�� ��ı��� |
| ��1�� | [18��28�� | 5 | 0.5 |
| ��2�� | [28��38�� | 18 | a |
| ��3�� | [38��48�� | 27 | 0.9 |
| ��4�� | [48��58�� | x | 0.36 |
| ��5�� | [58��68] | 3 | 0.2 |
���� �����������1������Ϊ10���ɴ������a��x��ֵ��
����2��3��4��ش���ȷ�������ı�Ϊ18��27��9=2��3��1���ɴ��������2��3��4��ÿ��Ӧ�����γ�ȡ��������
���ǡ�����ȡ�����е�2��������1�˻�����˽���Ϊ�¼�A����ȡ��6���У���2 �����Ϊa1��a2����3�����Ϊb1��b2��b3����4�����Ϊc�������оٷ������6������������ȡ2�������п��ܵ������15�֣��������оٷ������2��������1�˵������9�֣��ɴ����������ȡ�����е�2��������1�˻�����˽��ĸ��ʣ�
��� �⣺����1������5��0.5=10��
����10��0.1=100��
��2��Ƶ��Ϊ��0.2������Ϊ��100��0.2=20��
����18��20=0.9������2�֣�
��4������100��0.25=25��
����x=25��0.36=9������4�֣�
����2��3��4��ش���ȷ�������ı�Ϊ18��27��9=2��3��1������5�֣�
���Ե�2��3��4��ÿ��Ӧ�����γ�ȡ2�ˣ�3�ˣ�1�ˣ�����7�֣�
���ǡ�����ȡ�����е�2��������1�˻�����˽���Ϊ�¼�A��
��ȡ��6���У���2 �����Ϊa1��a2����3�����Ϊb1��b2��b3��
��4�����Ϊc�����6������������ȡ2�������п��ܵ������15�֣������ǣ�
��a1��a2������a1��b1������a1��b2������a1��b3������a1��c������a2��b1������a2��b2������a2��b3����
��a2��c������b1��b2������b1��b3������b1��c������b2��b3������b2��b3������b2��c������b3��c���� ����9�֣�
���е�2��������1�˵������9�֣�
�����ǣ���a1��a2������a1��b1������a1��b2������a1��b3������a1��c����
��a2��b1������a2��b2������a2��b3������a2��c���� ����10�֣�
����ȡ�����е�2��������1�˻�����˽��ĸ���p��A��=$\frac{9}{15}$=$\frac{3}{5}$�� ����12�֣�
���� ���⿼��ֲ������Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������x�ʣ�0��+�ޣ�������lnx��x-2 | B�� | ������x�ʣ�0��+�ޣ�������lnx��x-2 | ||
| C�� | ����x�ʣ�0��+�ޣ���ʹ��lnx��x-2 | D�� | ����x�ʣ�0��+�ޣ���ʹ��lnx��x-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{4}{3}$ | B�� | $\frac{8}{3}$ | C�� | 4 | D�� | $6+2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����Ϊa1����С��Ϊa3 | B�� | �����Ϊa1����С����� | ||
| C�� | �������ڡ���С��Ϊa3 | D�� | �����Ϊa1����С��Ϊa4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 2$\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com