
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 由题意可得F2($\sqrt{2}$,0),F1 (-$\sqrt{2}$,0),由余弦定理可得 PF1•PF2=4,由${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$PF1•PF2sin60°,计算即可得到所求.
解答 解:由双曲线x2-y2=1的a=b=1,c=$\sqrt{2}$,
F2($\sqrt{2}$,0),F1 (-$\sqrt{2}$,0),
由余弦定理可得,
F1F22=8=PF12+PF22-2PF1•PF2cos60°
=(PF1-PF2)2+PF1•PF2=4+PF1•PF2,
∴PF1•PF2=4.
则${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$PF1•PF2sin60°=$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
故选C.
点评 本题考查双曲线的定义和标准方程,余弦定理,以及双曲线的简单性质的应用,求出PF1•PF2的值,是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
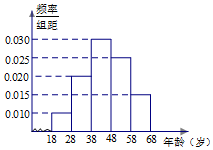 某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68],再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68],再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.| 组号 | 分组 | 回答正确的人数 | 回答正确 的人数占本 组的比例 |
| 第1组 | [18,28) | 5 | 0.5 |
| 第2组 | [28,38) | 18 | a |
| 第3组 | [38,48) | 27 | 0.9 |
| 第4组 | [48,58) | x | 0.36 |
| 第5组 | [58,68] | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
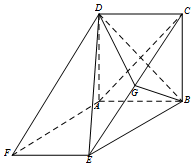 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com