
如图,已知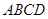 为平行四边形,
为平行四边形,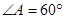 ,
,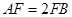 ,
,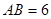 ,点
,点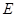 在
在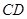 上,
上,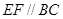 ,
, ,
,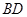 与
与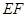 相交于
相交于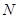 .现将四边形
.现将四边形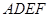 沿
沿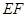 折起,使点
折起,使点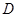 在平面
在平面 上的射影恰在直线
上的射影恰在直线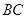 上.
上.
(1)求证: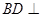 平面
平面 ;
;
(2)求折后直线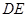 与平面
与平面 所成角的余弦值.
所成角的余弦值.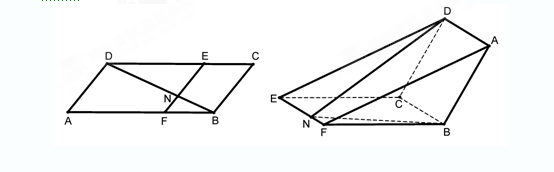
(1)(2)
解析试题分析:(1)连接 ,欲证
,欲证 平面
平面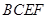 ,只要证点
,只要证点 是点
是点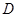 在平面
在平面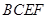 内的射影,易证在平面图中,
内的射影,易证在平面图中,
有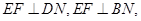 此结论在折后的空间几何体中仍成立
此结论在折后的空间几何体中仍成立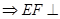 平面
平面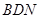
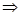 平面
平面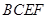
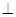 平面
平面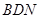
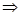 点
点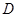 在平面
在平面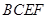 内的射影在直线
内的射影在直线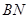 上,结合已知条件,知点
上,结合已知条件,知点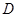 在平面
在平面 上的射影又恰在直线
上的射影又恰在直线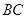 上
上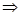
 是点
是点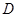 在平面
在平面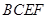 内的射影,从而结论得证.利用勾股定理求出相关线段的长度即可在直角三角形
内的射影,从而结论得证.利用勾股定理求出相关线段的长度即可在直角三角形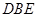 求出
求出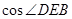 的值.
的值.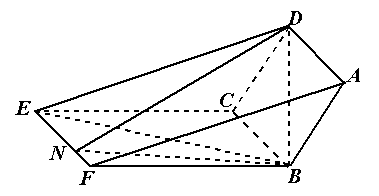
(2)连接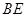 ,由(1)知,
,由(1)知,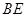 是
是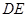 在平面
在平面 内的射影,
内的射影,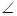
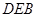 就是所求的线面角,
就是所求的线面角,
试题解析:(1)由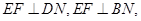 得
得 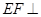 平面
平面 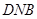
则平面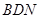
 平面
平面 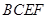
 平面
平面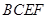
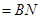
则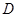 在平面
在平面 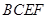 上的射影在直线
上的射影在直线 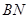 上,
上,
又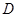 在平面
在平面 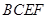 上的射影在直线
上的射影在直线 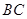 上,
上,
则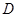 在平面
在平面 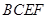 上的射影即为点
上的射影即为点  ,
,
故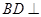 平面
平面 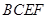
(2)连接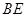 ,由
,由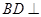 平面
平面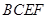 ,得
,得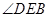 即为直线
即为直线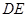 与平面
与平面 所成的角,
所成的角,
在原图中,由已知,可得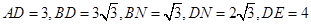
折后,由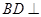 平面
平面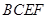 ,知
,知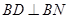
则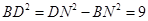 ,即
,即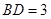
则在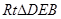 中,有
中,有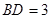 ,
,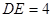 ,则
,则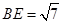 ,
,
故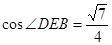
即折后直线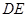 与平面
与平面 所成角的余弦值为
所成角的余弦值为


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
如图, ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF= AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.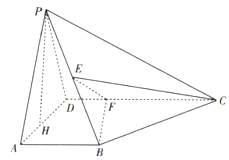
(1)证明:PH⊥平面ABCD;
(2)若PH=1,AD=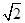 ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积;
(3)证明:EF⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,长方体 中,
中, ,G是
,G是 上的动点。
上的动点。
(l)求证:平面ADG
 ;
;
(2)判断 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;
(3)若G是 的中点,求二面角G-AD-C的大小;
的中点,求二面角G-AD-C的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知三棱锥P-ABC中,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB中点,且△PDB是正三角形,PA⊥PC。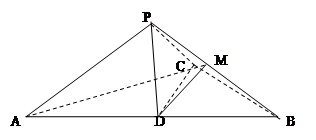 .
.
(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱锥S ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com