




 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 资 金 | 单位产品所需资金(百元) | 资金供应量 (百元) | |
| 洗衣机 | 空 调 | ||
| 成 本 | 20 | 30 | 300 |
| 工 资 | 10 | 5 | 110 |
| 单位利润 | 8 | 6 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
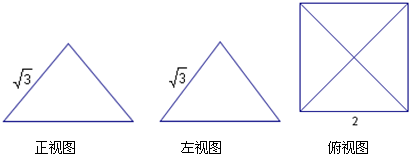
查看答案和解析>>
科目:高中数学 来源: 题型:
 某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 5-2x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
| B、8 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
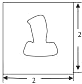 某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为
某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com