
已知椭圆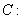
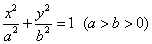 的左、右焦点分别为
的左、右焦点分别为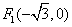 、
、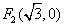 ,
,
椭圆上的点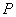 满足
满足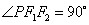 ,且
,且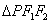 的面积
的面积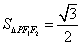 .
.
(Ⅰ)求椭圆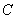 的方程;
的方程;
(Ⅱ)是否存在直线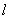 ,使
,使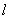 与椭圆
与椭圆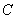 交于不同的两点
交于不同的两点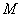 、
、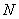 ,且线段
,且线段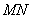 恰被直线
恰被直线
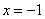 平分?若存在,求出
平分?若存在,求出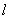 的斜率取值范围;若不存在,请说明理由.
的斜率取值范围;若不存在,请说明理由.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com