
分析 (1)由f(-x)=-f(x),代入可求b,然后由且f($\frac{1}{2}$)=$\frac{2}{5}$可求a,进而可求函数解析式;
(2)利用函数单调性的定义进行证明;
(3)利用函数奇偶性和单调性的性质将不等式进行转化进行求解即可.
解答 解:(1)∵函数f(x)=$\frac{ax+b}{1+{x}^{2}}$是定义在(-1,1)上的奇函数,
∴f(-x)=-f(x),即 $\frac{-ax+b}{1+{x}^{2}}=-\frac{ax+b}{1+{x}^{2}}$,
∴-ax+b=-ax-b,∴b=0,
∵f($\frac{1}{2}$)=$\frac{2}{5}$,
∴$\frac{\frac{1}{2}a}{1+(\frac{1}{2})^{2}}=\frac{2}{5}$,解得a=1,
∴f(x)=$\frac{x}{1+{x}^{2}}$.
(2)证明:在区间(-1,1)上任取x1,x2,令-1<x1<x2<1,
∴f(x1)-f(x2)=$\frac{{x}_{1}}{1+{{x}_{1}}^{2}}$-$\frac{{x}_{2}}{1+{{x}_{2}}^{2}}$=$\frac{({x}_{1}-{x}_{2})(1-{x}_{1}{x}_{2})}{(1+{{x}_{1}}^{2})(1+{{x}_{2}}^{2})}$;
∵-1<x1<x2<1
∴x1-x2<0,1-x1x2>0,1+x12>0,1+x22>0
∴f(x1)-f(x2)<0即f(x1)<f(x2)
故函数f(x)在区间(-1,1)上是增函数.
(3)∵f(x)是奇函数,
∴不等式f(t-1)+f(t)<0等价为f(t-1)<-f(t)=f(-t),
∵函数f(x)在区间(-1,1)上是增函数,
∴$\left\{\begin{array}{l}{-1<t<1}\\{-1<t-1<1}\\{t-1<-t}\end{array}\right.$,即$\left\{\begin{array}{l}{-1<t<1}\\{0<t<2}\\{t<\frac{1}{2}}\end{array}\right.$,解得0<t<$\frac{1}{2}$,
即不等式的解集为(0,$\frac{1}{2}$).
点评 本题考查函数奇偶性与单调性的性质应用,着重考查学生理解函数奇偶性与用定义证明单调性及解方程,解不等式组的能力,属于中档题.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
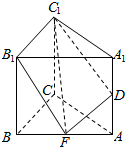 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -5 | C. | 15 | D. | -15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
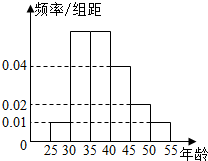 为响应工业园区举行的万人体质监测活动,某高校招募了N名志愿服务者,将所有志愿者按年龄情况分为25~30,30~35,35~40,45~50,50~55六个层次,其频率分布直方图如图所示,已知35~45之间的志愿者共20人.
为响应工业园区举行的万人体质监测活动,某高校招募了N名志愿服务者,将所有志愿者按年龄情况分为25~30,30~35,35~40,45~50,50~55六个层次,其频率分布直方图如图所示,已知35~45之间的志愿者共20人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥$\frac{5}{4}$ | B. | k>-$\frac{5}{4}$ | C. | k≤-$\frac{5}{4}$ | D. | k<-$\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com