
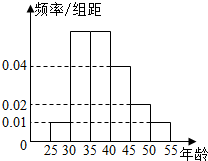
 为响应工业园区举行的万人体质监测活动,某高校招募了N名志愿服务者,将所有志愿者按年龄情况分为25~30,30~35,35~40,45~50,50~55六个层次,其频率分布直方图如图所示,已知35~45之间的志愿者共20人.
为响应工业园区举行的万人体质监测活动,某高校招募了N名志愿服务者,将所有志愿者按年龄情况分为25~30,30~35,35~40,45~50,50~55六个层次,其频率分布直方图如图所示,已知35~45之间的志愿者共20人.分析 (1)通过频率分布直方图,即可计算出N;
(2)从6名志愿者中抽取2名志愿者有15种情况,其中恰好抽到1名女教师,1名男教师共有8种,再利用古典概型的概率计算公式即可得出.
解答 解:(1)由题知35~40的频率为$\frac{1}{2}$[1-(0.01+0.02+0.04+0.01)×5]=0.3,
∴35~40的频率为0.3+0.04×5=0.5,
∴N=$\frac{20}{0.5}$=40,
(2)45~55之间的志愿者中女教师有4名,男教师有40×(0.01+0.02)×5-2=2名,
记4名女教师为A1,A2,A3,A4,2名男教师为B1B2,则从6名志愿者中抽取2名志愿者有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),
(A3,A4),(A3,B1),(A3,B2),
(A4,B1),(A4,B2),
(B1,B2),共有15种.
其中恰好抽到1名女教师,1名男教师共有8种,
故恰好抽到1名女教师,1名男教师的概率$\frac{8}{15}$.
点评 本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | M?N | C. | M=N | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 0.5 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com