
观察下列各不等式:
1+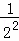 <,
<,
1+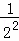 +
+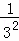 <,
<,
1+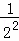 +
+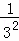 +
+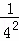 <,
<,
1+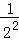 +
+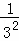 +
+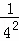 +
+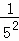 <,
<,
…
(1)由上述不等式,归纳出一个与正整数n(n≥2)有关的一般性结论;
(2)用数学归纳法证明你得到是结论.
科目:高中数学 来源: 题型:
如果某年年份的各位数字之和为7,我们称该年为“七巧年”.例如,今年年份2014的各位数字之和为7,所以今年恰为“七巧年”,那么从2000年到2999年中“七巧年”共有 _________ 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com