
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| 6 |
| 30 |
| 1 |
| 5 |
| 1 |
| 5 |
| 8 |
| 15 |


科目:高中数学 来源: 题型:
| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩手机游戏 | 18 | 2 | |
| 不喜欢玩手机游戏 | 6 | ||
| 合计 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
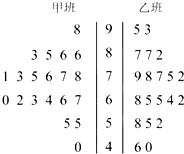 某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.
某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:
| a1 | a1 |
| a2 | a2 |
| an | an |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| α |
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
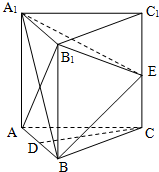 如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
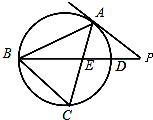 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com