Question

15．已知斜四棱柱ABCD-A₁B₁C₁D₁的底面是矩形，侧面CC₁D₁D垂直底面ABCD，BC=2AB=DC₁=2，BD₁=2$\sqrt{3}$．
（1）求证：平面AB₁C₁D⊥平面ABCD；
（2）点E是棱BC的中点，求二面角A₁-AE-D的余弦值．

Answer 1

分析 （1）连结CD₁，利用线面垂直的性质定理、勾股定理及面面垂直的判定定理即得结论；
（2）以D为原点，以DA、DC、DC₁所在直线分别为x、y、z轴建立空间坐标系，则所求值转化为平面DAE的法向量与平面A₁AE的法向量的夹角的余弦值的绝对值．

解答 （1）证明：连结CD₁，设CD₁∩DC₁=F，则F是CD₁、DC₁的中点，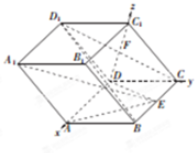
∵底面ABCD是矩形，∴BC⊥CD，
又∵平面CC₁D₁D⊥平面ABCD，∴平面CC₁D₁D⊥BC，∴BC⊥CD₁，
∵BC=2，BD₁=2$\sqrt{3}$，∴CD₁=2$\sqrt{2}$，CF=$\sqrt{2}$，
在△DFC中，DF=$\frac{1}{2}$DC₁=1，CD=1，
∴CD²+DF²=CF²，∴DF⊥DC，
又BC⊥平面CC₁D₁D，∴DF⊥BC，
∴DF⊥平面ABCD，DF?平面AB₁C₁D，
∴平面AB₁C₁D⊥平面ABCD；
（2）解：由（1）知能以D为原点，以DA、DC、DC₁所在直线分别为x、y、z轴建立空间坐标系，
则平面DAE的法向量为$\overrightarrow{n}$=$\overrightarrow{D{C}_{1}}$=（0，0，2），
设平面A₁AE的法向量为$\overrightarrow{m}$=（x，y，z），
∵$\overrightarrow{DA}$=（2，0，0），$\overrightarrow{DE}$=（1，1，0），$\overrightarrow{A{A}_{1}}$=$\overrightarrow{D{D}_{1}}$=（0，-1，2），
∴$\overrightarrow{AE}$=（-1，1，0），
∴$\left\{\begin{array}{l}{-x+y=0}\\{-y+2z=0}\end{array}\right.$，
令z=1，得$\overrightarrow{m}$=（2，2，-1），
∴cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞=$\frac{2}{\sqrt{4+4+1}×2}$=$\frac{1}{3}$，
即所求二面角的余弦值为$\frac{1}{3}$．

点评 本题考查二面角，空间中面面的位置关系，向量数量积运算，注意解题方法的积累，建立坐标系是解决本题的关键，属于中档题．