练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】把函数y=cos（2x+φ）（|φ|＜ ）的图象向左平移 个单位，得到函数y=f（x）的图象关于直线x= 对称，则φ的值为（ ）
    A.﹣
    B.﹣
    C.
    D.

    【答案】B
    【解析】解：把函数y=cos（2x+φ）（|φ|＜ ）的图象向左平移 个单位，得到函数y=f（x）=cos[2（x+ ）+φ]=cos（2x+φ+ ）的图象关于直线x= 对称，
    则2× +φ+ =kπ，求得φ=kπ﹣ ，k∈Z，故φ=﹣ ，
    故选：B．
    【考点精析】掌握函数y=Asin（ωx+φ）的图象变换是解答本题的根本，需要知道图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知x，y满足约束条件 ，若z=y﹣ax取得最大值的最优解不唯一，则实数a的值为（ ）
    A. 或﹣1
    B.2或
    C.2或﹣1
    D.2或1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解高中生作文成绩与课外阅读量之间的关系，某研究机构随机抽取了60名高中生，通过问卷调查，得到以下数据：

    0.050

    0.025

    0.010

    0.005

    0.001

    k

    3.841

    5.024

    6.635

    7.879

    10.828

    由以上数据，计算得到K2的观测值k≈9.643，根据临界值表，以下说法正确的是(　　)

    A. 没有充足的理由认为课外阅读量大与作文成绩优秀有关

    B. 有0.5%的把握认为课外阅读量大与作文成绩优秀有关

    C. 有99.9%的把握认为课外阅读量大与作文成绩优秀有关

    D. 有99.5%的把握认为课外阅读量大与作文成绩优秀有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cos2ωx+2 sinωxcosωx﹣1，且f（x）的周期为2．
    （Ⅰ）当 时，求f（x）的最值；
    （Ⅱ）若 ，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f′（x）是奇函数f（x）（x∈R）的导函数，f（﹣1）=0，当x＞0时，xf′（x）﹣f（x）＜0，则使得f（x）＞0成立的x的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，网格纸上小正方形的边长为1，粗线画出的是一正方体被截去一部分后所得几何体的三视图，则该几何体的表面积为（ ）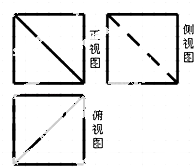

    A.54
    B.162
    C.54+18
    D.162+18

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+alnx．

    （1）若a=﹣1，求函数f（x）的极值，并指出极大值还是极小值；

    （2）若a=1，求函数f（x）在[1，e]上的最值；

    （3）若a=1，求证：在区间[1，+∞）上，函数f（x）的图象在g（x）=x3的图象下方．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义域为R的函数f（x）对任意x∈R都有f（x）=f（4﹣x），且其导函数f′（x）满足（x﹣2）f′（x）＞0，则当2＜a＜4时，有（ ）
    A.f（2a）＜f（2）＜f（log2a）
    B.f（2）＜f（2a）＜f（log2a）
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力．每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训．已知参加过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响．

    （1）任选1名下岗人员，求该人参加过培训的概率；

    （2）任选3名下岗人员，记ξ为3人中参加过培训的人数，求ξ的分布列．

    查看答案和解析>>

    同步练习册答案