
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据直线和圆相交的性质,结合充分条件和必要条件的定义进行判断即可得到结论.
解答 解:若直线l:y=kx+1与圆O:x2+y2=1相交于A,B 两点,
则圆心到直线距离d=$\frac{1}{\sqrt{1+{k}^{2}}}$,|AB|=2$\sqrt{1-{d}^{2}}=2\sqrt{1-\frac{1}{1+{k}^{2}}}=2\sqrt{\frac{{k}^{2}}{1+{k}^{2}}}$,
若k=$\sqrt{3}$,则|AB|=$\sqrt{3}$,d=$\frac{1}{\sqrt{1+3}}=\frac{1}{2}$,则△OAB的面积为$\frac{1}{2}$×$\frac{1}{2}×\sqrt{3}$=$\frac{\sqrt{3}}{4}$成立,即必要性成立.
若△OAB的面积为$\frac{{\sqrt{3}}}{4}$,则S=$\frac{1}{2}×\frac{1}{\sqrt{1+{k}^{2}}}×2\sqrt{\frac{{k}^{2}}{1+{k}^{2}}}$=$\frac{|k|}{1+{k}^{2}}$=$\frac{{\sqrt{3}}}{4}$,
解得k=±$\sqrt{3}$,则k=$\sqrt{3}$不成立,即充分性不成立.
故“△OAB的面积为$\frac{{\sqrt{3}}}{4}$”是“k=$\sqrt{3}$”的必要不充分条件.
故选:B.
点评 本题主要考查充分条件和必要条件的判断,利用三角形的面积公式,以及半径半弦之间的关系是解决本题的关键.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y=f(x) | 3 | 0 | 1 | 2 |
| x | 0 | 1 | 2 | 3 |
| y=g(x) | 1 | 0 | 3 | 2 |
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.
为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
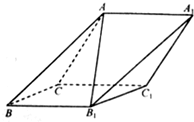 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com