
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
���� ���������ı������������ݵ�ƽ������һ��ƽ�����룬�����ķ����DZ����ƽ�����жϢ���ȷ��
������ֵΪa�Ĺ�Ʊ����10����ͣ���µ�10%�����پ���10����ͣ������10%��������ֵΪa����1-$\frac{1}{10}$����1+$\frac{1}{10}$��=$\frac{99}{100}$a���жϢڴ���
�����������������ѧƽ���ֿ��жϢ۴���
����ֶμ��Ϊ16����503=61��31+7���ɵõ�һ����ȡ�ĺ���Ϊ007���жϢ���ȷ��
��� �⣺���ڢ٣������ı������������ݵ�ƽ������һ��ƽ�����룬�����ķ����DZ����ƽ������ӳ���������ݵķ�ɢ�̶ȵĴ�С���ʢ���ȷ��
���ڢڣ����Ʊ��ֵΪa����Ʊ����10����ͣ���µ�10%�����پ���10����ͣ������10%��������ֵΪa����1-$\frac{1}{10}$����1+$\frac{1}{10}$��=$\frac{99}{100}$a���ʢڴ���
���ڢۣ��߸���һ�����Ͷ��������ֱַܷ�Ϊ��ma��nb��������Ϊm+n������������������ѧƽ����Ϊ$\frac{ma+nb}{m+n}$���ʢ۴���
���ڢܣ�����ϵͳ������������ȫ��800��ѧ���г�50��ѧ���ķֶμ��Ϊ$\frac{800}{50}$=16��
�ִ�497��512��16������ȡ�õ�ѧ�������503����503=16��31+7�����ڵ�1С��1��l6������鵽��ѧ�������007�ţ��ʢ���ȷ��
��������ĸ�����2����
��ѡ��C��
���� ���⿼����ϵͳ���������������ķ���ĺ��弰�ڻع����ģ���вв�ƽ���͵ĺ��壬������ѧ������������������������ո���ͳ�ƻ���֪ʶ�ǽ����Ĺؼ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ֱ����ABCD-A1B1C1D1�У�����ABCD��ֱ�����Σ���BAD=��ADC=90�㣬AB=2AD=2CD=2��
ֱ����ABCD-A1B1C1D1�У�����ABCD��ֱ�����Σ���BAD=��ADC=90�㣬AB=2AD=2CD=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+i | B�� | 1-i | C�� | -1+i | D�� | -1-i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
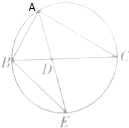 ��ͼ����Rt��ABC�У�ֱ��A�Ľ�ƽ����AD���ӳ��߽��������Բ�ڵ�E��AD=1.6��AE=3��
��ͼ����Rt��ABC�У�ֱ��A�Ľ�ƽ����AD���ӳ��߽��������Բ�ڵ�E��AD=1.6��AE=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com