
【题目】如图,已知梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,矩形
,矩形![]()
![]() 平面
平面![]() ,且
,且![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求证:![]() ∥平面
∥平面![]() ;
;
(3)求二面角![]() 的正切值.
的正切值.
【答案】(1)证明见解析;(2)证明见解析;(3) ![]()
【解析】
(1)根据面面垂直的性质定理证得![]() 平面
平面![]() ,从而可得
,从而可得![]() ,再根据
,再根据![]() 以及线面垂直的判定定理可得.
以及线面垂直的判定定理可得.![]() 平面,从而可得
平面,从而可得![]() .
.
(3) 过点B作![]() 垂足为
垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则
,则![]() 就是所求二面角
就是所求二面角![]() 的平面角,在三角形
的平面角,在三角形![]() 中,可求得答案.
中,可求得答案.
解:(1)![]() 矩形
矩形![]()
![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() =CD ,又
=CD ,又![]() 平面
平面![]() .
.
![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
![]() ,
,
![]() 且
且![]() ,
,
.![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
则![]()
(2)如图所示:

取![]() 中点M,连接
中点M,连接![]() ,由已知条件易得
,由已知条件易得![]() 及
及![]() 为平行四边形,于是
为平行四边形,于是![]() ,由于
,由于![]() ,故
,故![]() 为平行四边形.
为平行四边形.
![]() .
.![]() 面ABE,
面ABE,
所以![]() 平面
平面![]() .又
.又![]() , 所以
, 所以![]() 面
面![]() ,
,
又![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() . 又
. 又![]() 平面
平面![]()
![]() ∥平面
∥平面![]() .
.
(3)如图所示:

过点B作![]() 垂足为
垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .由矩形
.由矩形![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,又
,又![]() ,
,![]()
所以![]() 就是所求二面角
就是所求二面角![]() 的平面角.
的平面角.
在△![]() 中,根据面积关系可得
中,根据面积关系可得![]() ,得
,得![]() ,得
,得![]() ,解得
,解得![]() .
.
在![]() 中,
中, ![]()
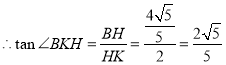 .
.
故二面角![]() 的正切值为
的正切值为![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5,该纸片上的等边三角形ABC的中心为O,点D,E,F为圆O上的点,![]() ,
,![]() ,
,![]() 分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起
分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起![]() ,
,![]() ,
,![]() ,使得D,E,F重合于P,得到三棱锥
,使得D,E,F重合于P,得到三棱锥![]() .
.

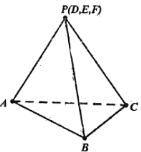
(1)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)当![]() 的边长变化时,三棱锥
的边长变化时,三棱锥![]() 的侧面和底面所成二面角为
的侧面和底面所成二面角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :
: ![]() 表示双曲线,命题
表示双曲线,命题![]() :
: ![]() 表示椭圆。
表示椭圆。
(1)若命题![]() 与命题
与命题![]() 都为真命题,则
都为真命题,则![]() 是
是![]() 的什么条件?
的什么条件?
(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
(2)若![]() 为假命题,且
为假命题,且![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动点![]() 分别与两个定点
分别与两个定点![]() ,
,![]() 的连线的斜率之积为
的连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() ,
,![]() 两点,判断直线
两点,判断直线![]() 与以线段
与以线段![]() 为直径的圆的位置关系,并说明理由.
为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥D-ABC中,二面角A-BC-D的大小为90°,且∠BDC=90°,∠ABC=30°,BC=3,![]() .
.
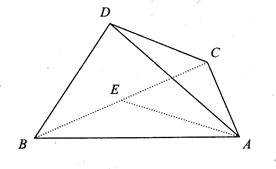
(1)求证:AC⊥平面BCD;
(2)二面角B-AC-D为45°,且E为线段BC的中点,求直线AE与平面ACD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x∈R,x2+2x≥a,q:x2﹣4x+3≤0,r:(x﹣m)[x﹣(m+1)]≤0.
(1)若命题p的否定是假命题,求实数a的取值范围;
(2)若q是r的必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且经过点
,且经过点![]() .
.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 过点
过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.若![]() ,则
,则![]() ,
,![]() 的长度相等,方向相同或相反
的长度相等,方向相同或相反
B.若向量![]() 是向量
是向量![]() 的相反向量,则
的相反向量,则![]()
C.空间向量的减法满足结合律
D.在四边形![]() 中,一定有
中,一定有![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com