
设a,b为正实数,现有下列命题:
①若a2-b2=1,则a-b<1;
②若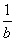 -
-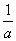 =1,则a-b<1;
=1,则a-b<1;
③若|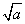 -
-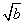 |=1,则|a-b|<1;
|=1,则|a-b|<1;
④若|a3-b3|=1,则|a-b|<1.
其中的真命题有________.(写出所有真命题的编号)
①④
[解析] 本题考查了等式与不等式之间的逻辑关系
对于①,由a2-b2=1,则(a-b)(a+b)=1,
则a-b>0故a>b,又a>0,b>0,则a+b>a-b,若a-b≥1,则a+b>1,则(a+b)(a-b)>1这与已知条件(a-b)(a+b)=1矛盾,故①成立.
对于②,不妨取a=2,b=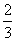 ,则a-b=2-
,则a-b=2-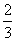 >1,
>1,
故②不正确.
对于③,不妨取a=9,b=4,则|a-b|=5>1,故③不正确,
对于④,由|a3-b3|=1知a≠b,不妨设a>b,若|a-b|≥1,而a≥b+1,又b>0,则a>1,∴a2+ab+b2>1,
由|a3-b3|=|a-b||a2+ab+b2|=|a-b|(a2+ab+b2)
故|a3-b3|>1,这与已知条件矛盾,
解决问题时直接去解不好处理的情况下可选择间接解法例如反证法,对于不正确命题可举一个反例即可.


科目:高中数学 来源: 题型:
已知直线l: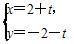 (t为参数)与圆C:
(t为参数)与圆C: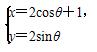 (θ为参数),则直线l的倾斜角及圆心C的直角坐标分别为( )
(θ为参数),则直线l的倾斜角及圆心C的直角坐标分别为( )
A. ,(1,0) B
,(1,0) B ,(-1,0)
,(-1,0)
C.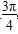 ,(1,0) D.
,(1,0) D.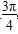 ,(-1,0)
,(-1,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|x+1|+|x-3|.
(1)作出函数y=f(x)的图象;
(2)若对任意x∈R,f(x)≥a2-3a恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题:“在等差数列{an}中,若4a2+a10+a( )=24,则S11为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
国家法定工作日内,每周工作时间满工作量为40h,每小时工资8元;如因需要加班,则每小时工资为10元.某人在一周内工作时间为xh,但他须交纳个人住房公积金、失业险(这两项费用为每周总收入的10%).试分析算法步骤并画出其净得工资y元的算法的流程图.(注:满工作量外的工作时间为加班)
查看答案和解析>>
科目:高中数学 来源: 题型:
下面程序的运行结果是( )
a=2
b=10
Do
a=a+1
b=b-1
Loop While b>8
输出a,b
A.2,10 B.3,9
C.4,8 D.4,7
查看答案和解析>>
科目:高中数学 来源: 题型:
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin13°cos17°;
②sin215°+cos215°-sin15°cos15°;
③sin218°+cos212°-sin18°cos12°;
④sin2(-18°)+cos248°-sin(-18°)cos48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos55°.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com