
分析 (1)可用反证法证明,假设存在满足ak=bk(k=1,2,…,n)的数列{an},由条件结合奇数、偶数的概念即可得证;
(2)由题意可得{ck}:n,n-1,n-2,…,1,再由累加法即可得到Sn;
(3)由(1-b1)2+(2-b2)2+…+(n-bn)2≥0,展开即可证得b1+2b2+…+nbn≤$\frac{1}{6}$n(n+1)(2n+1);再由排序定理:乱序之和不小于倒序之和.
解答 解:(1)证明:当n为正偶数时,
存在满足ak=bk(k=1,2,…,n)的数列{an},
由bk=n+1-ak(k=1,2,…,n),可得
ak=$\frac{n+1}{2}$,由n为正偶数,可得n+1为奇数,
$\frac{n+1}{2}$不为整数,ak为整数,故不成立,
则当n为正偶数时,
不存在满足ak=bk(k=1,2,…,n)的数列{an};
(2){ck}:n,n-1,n-2,…,1,
由S1=1,S2-S1=3,S3-S2=6,S4-S3=10,…,Sn-Sn-1=3+$\frac{(n-2)(n+3)}{2}$,n>1.
累加可得,Sn=1+3+6+10+…+[3+$\frac{(n-2)(n+3)}{2}$]=$\frac{1}{2}$(12+22+…+n2)+(1+2+…+n)]
=$\frac{1}{2}$×$\frac{1}{6}$n(n+1)(2n+1)+$\frac{1}{4}$n(n+1)=$\frac{1}{6}$n(n+1)(n+2);
(3)证明:由(1-b1)2+(2-b2)2+…+(n-bn)2≥0,可得
12+22+…+n2-2(b1+2b2+…+nbn)+(b12+b22+…+bn2)≥0,
即有b1+2b2+…+nbn≤$\frac{1}{2}$[(12+22+…+n2)+(b12+b22+…+bn2)]
=12+22+…+n2=$\frac{1}{6}$n(n+1)(2n+1);
由排序定理可得,乱序之和不小于倒序之和,
由a1+2a2+…+nan为乱序之和,Sn=c1+2c2+…+ncn为倒序之和.
即可得到a1+2a2+…+nan≥Sn.
点评 本题考查数列的求和方法,以及数列不等式的证明,考查反证法的运用和综合法的运用,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}{π^2}}}{4}-1$ | B. | $\frac{{3{π^2}}}{4}-1$ | C. | $\frac{{3{π^2}}}{2}-1$ | D. | $\frac{π^2}{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
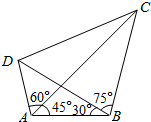 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com