
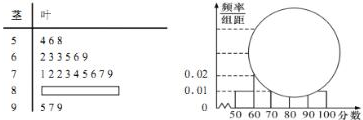
 某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;分析 (Ⅰ)根据分数在[50,60)的频率为0.01×10,和由茎叶图知分数在[50,60)之间的频数为3,得到全班人数.
(2)分数在[80,90)之间的频数为30-3-6-9-3,做出频率,根据小长方形的高是频率比组距,得到结果.
(Ⅲ)用各矩形中点的横坐标乘以本段的频率作和.
解答 解:(1)分数在[50,60)的频率为0.01×10=0.1,
由茎叶图知:分数在[50,60)之间的频数为3,所以全班人数为30;
(2)分数在[80,90)之间的频数为30-3-6-9-3=9,
频率分布直方图中[80,90)间的矩形的高为9÷30÷10=0.03;
(Ⅲ)$\overline{x}$=55×0.1+65×$\frac{6}{30}$+75×$\frac{9}{30}$+85×$\frac{9}{30}$+95×$\frac{3}{30}$=76,
所以该班数学成绩的平均分数估计为76分.
点评 本题考查了频率分布直方图,考查了茎叶图,频率分布直方图中,各矩形的面积和等于1,频率分布直方图中,平均数的估计值是各矩形中点的横坐标与对应频率乘积的和,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{2}}{9}$ | B. | -$\frac{4\sqrt{2}}{9}$ | C. | $\frac{7}{9}$ | D. | -$\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com