
分析 直接利用诱导公式以及两角和与差的正切函数化简求解即可.
解答 解:$\frac{3cos(\frac{π}{2}+α)-cos(π-α)}{sin(α-\frac{π}{2})-3sin(π+α)}$=$\frac{-3sinα+cosα}{-cosα+3sinα}$=-1.
tan25°+tan35°+$\sqrt{3}$tan25°tan35°=tan60°(1-tan25°tan35°)+$\sqrt{3}$tan25°tan35°
=$\sqrt{3}$-$\sqrt{3}$tan25°tan35°+$\sqrt{3}$tan25°tan35°
=$\sqrt{3}$.
故答案为:-1,$\sqrt{3}$.
点评 本题考查同角三角函数基本关系式以及两角和与差的正切函数的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
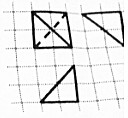 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )| A. | 2$\sqrt{2}$π | B. | 3$\sqrt{3}$π | C. | 4π | D. | 2$\sqrt{5}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
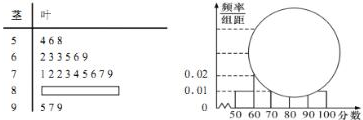 某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com