
���� ���ݺ����Ķ����϶��κ��������жϣ�1�������ݺ����ĵ����жϣ�2�����������Ǻ����������жϣ�3�������ݶ����жϣ�4�����ɣ�
��� �⣺��1������κ���f��x��=x2+mx+n������[a��b]���ǡ�������������
��f�䣨x1��=f�䣨x2��=2x1+m=2x2+m����x1=x2���붨�岻����
�ʶ��κ���f��x��=x2+mx+n����������[a��b]�϶��������ǡ���������������1����ȷ��
��2���ߺ���f��x��=$\frac{1}{3}$x3-x2+2��
��f�䣨x��=x2-2x��$\frac{f��a��-f��b��}{a-b}$=$\frac{f��0��-f��2��}{0-2}$=$\frac{2-��\frac{8}{3}-2��}{0-2}$=-$\frac{2}{3}$��
��x2-2x=-$\frac{2}{3}$����ã�x1=$\frac{3-\sqrt{3}}{3}$��x2=$\frac{3+\sqrt{3}}{3}$��
��0��x1��x2��2��
��f��x����[0��2]�ϵġ���������������2����ȷ��
��3���ߺ���f��x��=x+sinx��
��f�䣨x��=1+cosx��$\frac{f��\frac{��}{6}��-f��\frac{11��}{6}��}{\frac{��}{6}-\frac{11��}{6}}$=$\frac{3}{5��}$-1��
��1+cosx=$\frac{3}{5��}$-1����cosx=$\frac{3}{5��}$-2��-1���⣬
��f��x��=x+sinx����[$\frac{��}{6}$��$\frac{11��}{6}$]�ϵġ���������������3������
��4��f��x��Ϊ[a��b]�ϵġ���������������f�䣨x��=0��[a��b]������������ȵ�ʵ����
��f��x����[a��b]�ϲ���������4����ȷ��
������ȷ��������Ϊ ��1������2������4����
�ʴ�Ϊ����1������2������4����
���� ������һ���¶��庯�����⣬����Ժ������ʵ������Ӧ�ã�����ʱ�����������f��x���ĵ��������ٽ��¶��庯��������ת��Ϊ�����������ʣ�������Ϻ�����������ȷ�����������������֮�������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
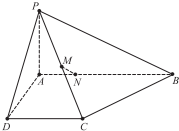 ��ͼ��������P-ABCD�У���֪AB��AD��AD��DC��PA�͵���ABCD����AB=2��PA=AD=DC=1��MΪPC���е㣬N��AB�ϣ���BN=3AN��
��ͼ��������P-ABCD�У���֪AB��AD��AD��DC��PA�͵���ABCD����AB=2��PA=AD=DC=1��MΪPC���е㣬N��AB�ϣ���BN=3AN���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 17 | C�� | 16 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
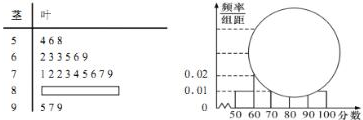 ijУ��һij���һ����ѧ���Գɼ�������Ϊ100�֣��ľ�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ���ܵ���ͬ�̶ȵ��ƻ������ɼ�������ͼ���ݴ˽���������⣻
ijУ��һij���һ����ѧ���Գɼ�������Ϊ100�֣��ľ�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ���ܵ���ͬ�̶ȵ��ƻ������ɼ�������ͼ���ݴ˽���������⣻�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x+y-5=0 | B�� | x+3y-7=0 | C�� | x-3y+5=0 | D�� | x-3y-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com