练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    下列四个命题中正确命题的个数是（ ）

    （1）三点确定一个平面

    （2）若点P不在平面α内，ABC三点都在平面α内，则P，A，B，C四点不共面

    （3）两两相交的三条直线在同一平面内

    （4）两组对边分别相等的四边形是平面图形．

    A.0 B.1 C.2 D.3

     

    A

    【解析】

    试题分析：由题意，四个命题都可根据公理3，研究确定一个平面的条件，由公理3及它的推论作出判断．

    【解析】
    由于过不共面的三点才能确定一个平面，故（1）不对；

    都在平面α内三点A、B、C，若三点共线，设它们共线于直线l，由直线l与点P可以确定一个平面，从而P，A，B，C四点共面，故（2）不正确；

    由于三条直线两两相交的情形中包括三线不共面且过一点的情形，这种情形中三线可确定三个平面，故三条直线两两相交则确定一个平面不正确，（3）不对；

    反例：菱形沿其中一条对角线折起后得到的空间四边形，故（4）不正确

    综上，四个命题中正确命题的个数是0．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2015年人教B版必修二2.1平面直角坐标系中的基本公式练习卷（解析版） 题型：解答题

    已知平行四边形的三个顶点A（﹣2，1），B（﹣1，3），C（3，4），求第四个顶点D的坐标．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷（解析版） 题型：

    已知三角形A（2，﹣1，4），B（3，2，﹣6），C（5，0，2），则①过A点的中线长为 ；②过B点的中线长为 ；③过C点的中线长为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2015人教B版选修4-5 3.2用数学归纳法证明不等式练习卷（解析版） 题型：选择题

    若命题P（n）对n=k成立，则它对n=k+2也成立，又已知命题P（2）成立，则下列结论正确的是（ ）

    A.P（n）对所有自然数n都成立

    B.P（n）对所有正偶数n成立

    C.P（n）对所有正奇数n都成立

    D.P（n）对所有大于1的自然数n成立

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷（解析版） 题型：

    下列说法正确的是（ ）

    A.平面α和平面β只有一个公共点

    B.两两相交的三条线共面

    C.不共面的四点中，任何三点不共线

    D.有三个公共点的两平面必重合

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷（解析版） 题型：

    在空间四点中，“四点不共面”是“任意三点不共线”的（ ）

    A.充分不必要条件 B.必要不充分条件

    C.充分必要条件 D.既不充分又不必要条件

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量（解析版） 题型：填空题

    已知矩阵的一个特征值为1则矩阵M的另一个特征值是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：填空题

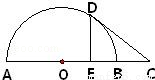
    （2014•东莞一模）如图，AB是半圆的直径，C是AB延长线上一点，CD切半圆于点D，CD=2，DE⊥AB，垂足为E，且E是OB的中点，则BC的长为 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理（解析版） 题型：选择题

    下列关于圆内接四边形叙述正确的有（ ）

    ①圆内接四边形的任何一个外角都等于它的内对角；

    ②圆内接四边形对角相等；

    ③圆内接四边形中不相邻的两个内角互补；

    ④在圆内部的四边形叫圆内接四边形．

    A.1个 B.2个 C.3个 D.4个

     

    查看答案和解析>>

    同步练习册答案