
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 根据$|\overrightarrow{a}|=1,|\overrightarrow{b}|=1$,对$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{3}|\overrightarrow{a}+\overrightarrow{b}|$两边平方即可求出$\overrightarrow{a}•\overrightarrow{b}$的值,进而求出$cos<\overrightarrow{a},\overrightarrow{b}>$的值,从而得出$\overrightarrow{a},\overrightarrow{b}$的夹角.
解答 解:由$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{3}|\overrightarrow{a}+\overrightarrow{b}|$得:
$(\overrightarrow{a}-\overrightarrow{b})^{2}=3(\overrightarrow{a}+\overrightarrow{b})^{2}$;
∴${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=3({\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2})$,且$|\overrightarrow{a}|=|\overrightarrow{b}|=1$;
∴$1-2\overrightarrow{a}•\overrightarrow{b}+1=3(1+2\overrightarrow{a}•\overrightarrow{b}+1)$;
解得$\overrightarrow{a}•\overrightarrow{b}=-\frac{1}{2}$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{1}{2}$;
∴$\overrightarrow{a},\overrightarrow{b}$夹角为$\frac{2π}{3}$.
故选:C.
点评 考查向量数量积的运算及计算公式,以及向量夹角的范围.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
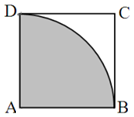 已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
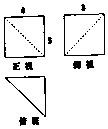 某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.
某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
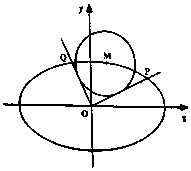 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
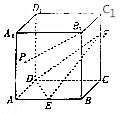 如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )| A. | [$\frac{1}{2}$,$\frac{3}{2}$] | B. | [0,1] | C. | [$\frac{1}{3}$,$\frac{\sqrt{10}}{3}$] | D. | [$\frac{1}{3}$,$\frac{\sqrt{13}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{2},\frac{5}{4}}]$ | B. | $[{0,\frac{5}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | (0,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com