
分析 ∠APC为锐角等价于cos∠APC>0,等价于$\overrightarrow{PA}$•$\overrightarrow{PC}$>0,根据向量数量积的坐标运算即可.
解答 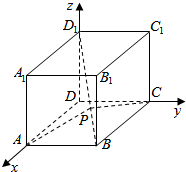 解:由题设可知,建立如图所示的空间直角坐标系D-xyz,
解:由题设可知,建立如图所示的空间直角坐标系D-xyz,
则有A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,1)
由$\overrightarrow{{D}_{1}B}$=(1,1,-1),得$\overrightarrow{{D}_{1}P}$=(λ,λ,-λ),
所以$\overrightarrow{PA}$=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),
$\overrightarrow{PC}$=(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),
所以∠APC为锐角等价于cos∠APC>0,
则等价于$\overrightarrow{PA}$•$\overrightarrow{PC}$>0,
即(1-λ)(-λ)+(-λ)(1-λ)+(λ-1)2=(λ-1)(3λ-1)>0,
∵0≤λ<1,∴,0≤λ<$\frac{1}{3}$
因此,λ的取值范围是$[{0,\frac{1}{3}})$,
故答案为$[{0,\frac{1}{3}})$.
点评 本题考查了用空间向量求直线间的夹角,一元二次不等式的解法,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
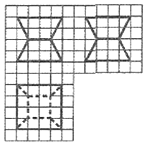 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3$\sqrt{2}$-2 | B. | 1 | C. | 3$\sqrt{2}$-1 | D. | -3$\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
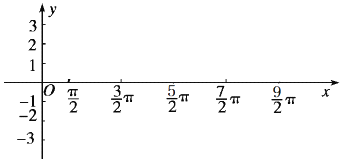
| $\frac{1}{2}$x-$\frac{π}{4}$ | |||||
| x | |||||
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com