
分析 根据三角函数的最值,求得a、b的值,可得f(x)的解析式,再利正弦函数的单调性求得$f(x)=bsin(ax+\frac{π}{3})$的递增区间.
解答 解:根据函数y=acosx+b的最大值为1,最小值为-3,可得-|a|+b=-3,|a|+b=1,
解得|a|=2,b=-1,
(1)当a>0时,a=2,b=-1,$f(x)=-sin(2x+\frac{π}{3})$,
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{12}$≤x≤kπ+$\frac{7π}{12}$,
可得函数的增区间为[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$],k∈Z.
(2)当a<0时,a=-2,b=-1,f(x)=-sin(-2x+$\frac{π}{3}$)=sin(2x-$\frac{π}{3}$),
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,
可得函数的增区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
点评 本题主要考查三角函数的最值,正弦函数的单调性,属于基础题.


科目:高中数学 来源: 题型:解答题
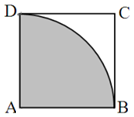 已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
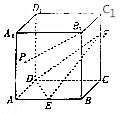 如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )| A. | [$\frac{1}{2}$,$\frac{3}{2}$] | B. | [0,1] | C. | [$\frac{1}{3}$,$\frac{\sqrt{10}}{3}$] | D. | [$\frac{1}{3}$,$\frac{\sqrt{13}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
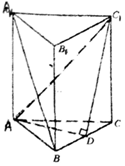 正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.
正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
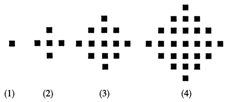 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{2},\frac{5}{4}}]$ | B. | $[{0,\frac{5}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 101 | B. | 808 | C. | 1212 | D. | 2012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com