
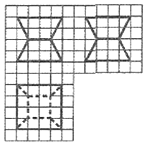
 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
分析 由已知中的三视图,可知该几何体是由一个棱长为4的正方体毛坯切削得到,该几何体是由两个正棱台对接可得,求出原来正方体的体积和该该几何体的体积,可得切削掉部分的体积与原毛坯体积的比值.
解答 解:由题意,该几何体是由一个棱长为4的正方体毛坯切削得到,该几何体是由两个全等的正棱台对接可得,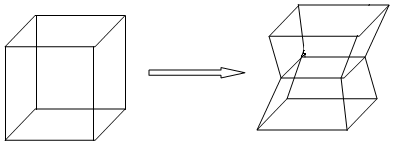
正棱台的下底为正方形,边长为4,上底为正方形,边长为2,高h为2,
可得:正棱台的体积V1=$\frac{1}{3}$h(S上+S下+$\sqrt{{S}_{下}•{S}_{上}}$)=$\frac{1}{3}×2$×(20+$\sqrt{16×4}$)=$\frac{56}{3}$
∴该几何体的体积V=$\frac{112}{3}$
棱长为4的正方体的体积V正=4×4×4=64.
切削掉部分的体积V′=64-$\frac{112}{3}$=$\frac{80}{3}$.
切削掉部分的体积与原毛坯体积的比值,即$\frac{80}{3}:64$=5:12,即$\frac{5}{12}$.
故选C
点评 本题考查了正方体的体积计算和正棱台的体积的计算,属于基础题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | m<-1 | B. | m=-1 | C. | m>-1 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
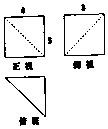 某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.
某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
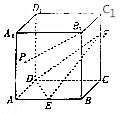 如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )| A. | [$\frac{1}{2}$,$\frac{3}{2}$] | B. | [0,1] | C. | [$\frac{1}{3}$,$\frac{\sqrt{10}}{3}$] | D. | [$\frac{1}{3}$,$\frac{\sqrt{13}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
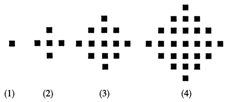 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com