
分析 逐次作出f1(x),f2(x),f3(x)的函数图象,观察f3(x)与函数y=$\frac{9}{8(x-1)}$图象交点的横坐标,作图求解即可.
解答 解:∵定义在R上的奇函数f(x),f(x+2)=f(x),
∴f(x)是周期为2的奇函数.
∵x∈[0,1]时,f(x)=1-|2x-1|.
∴函数f1(x)的图象如下图所示:
∵f2(x)=f(f1(x)),
∴函数f2(x)的图象如下图所示: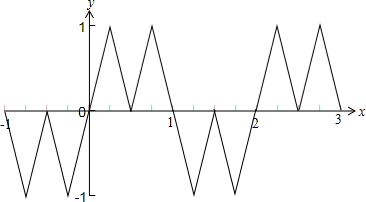
∵f3(x)=f(f2(x)),
∴作函数f3(x)与函数y=$\frac{9}{8(x-1)}$图象如下图所示: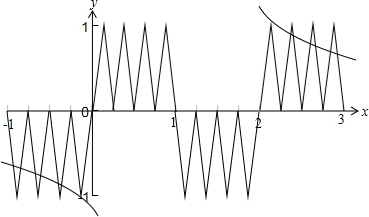
由图可知两函数图象共有14个交点,且两两关于(1,0)点对称,
故f3(x)=$\frac{9}{8(x-1)}$在[-1,3]内所有不等实根的和为14.
故答案为14.
点评 本题考查的知识点是函数的零点个数与方程根的关系,本题图象比较难画,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,2] | C. | (-∞,2] | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
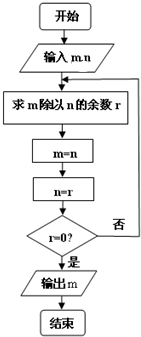 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )| A. | 3 | B. | 7 | C. | 0 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com