
分析 (I)利用导数判断f(x)的单调性,求出f(x)的最小值fmin(x),令fmin(x)≤0解出b的范围;
(II)f′(x)=(2x+1)(lnx+3x-a),设x0为h(x)=lnx+3x-a的零点,得出a,b关于x0的表达式及f(x)的单调性,从而得出b-2a关于x0的函数,根据x0的范围再计算函数的最小值.
解答 解:(I)a=3时,f(x)=(x2+x)lnx+2x3-2x2-4x+b,x∈(0,+∞),
∴f′(x)=(2x+1)lnx+(x2+x)$•\frac{1}{x}$+6x2-4x-4
=(2x+1)lnx+6x2-3x-3=(2x+1)lnx+(2x+1)(3x-3)
=(2x+1)(lnx+3x-3),
设g(x)=lnx+3x-3,则g(x)在(0,+∞)上单调递增,且g(1)=0,
∴当0<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴f(x)的最小值为f(1)=-4+b,
∵函数f(x)存在零点,且x→+∞时,f(x)→+∞,
∴-4+b≤0,解得b≤4.
(II)f′(x)=(2x+1)lnx+(x2+x)$•\frac{1}{x}$+6x2+2(1-a)x-a-1
=(2x+1)(lnx+3x-a),
令h(x)=lnx+3x-a,则h(x)在(0,+∞)上单调递增,
又x→0时,h(x)→-∞,当x→+∞时,h(x)→+∞,
∴存在唯一一个x0∈(0,+∞),使得h(x0)=0,即a=3x0+lnx0.
当0<x<x0时,f′(x)<0,当x>x0时,f′(x)>0,
∴f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增.
∴fmin(x)=f(x0)=(x02+x0)lnx0+2x03+(1-a)x02-(a+1)x0+b
=(x02+x0)lnx0+2x03+(1-3x0-lnx0)x02-(3x0+lnx0+1)x0+b
=-x03-2x02-x0+b.
∵f(x)≥0恒成立,
∴-x03-2x02-x0+b≥0,即b≥x03+2x02+x0.
∴b-2a≥x03+2x02+x0-2a=x03+2x02+x0-6x0-2lnx0=x03+2x02-5x0-2lnx0,
设φ(x)=x3+2x2-5x-2lnx,x∈(0,+∞),
则φ′(x)=3x2+4x-5-$\frac{2}{x}$=3x(x-1)+$\frac{7{x}^{2}-5x-2}{x}$=$\frac{(x-1)(3{x}^{2}+7x+2)}{x}$,
∴当0<x<1时,φ′(x)<0,当x>1时,φ′(x)>0,
∴φ(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴φ(x)≥φ(1)=-2.
∴当x0=1时,即a=3x0+lnx0=3,b=x03+2x02+x0=4时,b-2a取得最小值-2.
点评 本题考查了导数与函数单调性的关系,函数最值得计算,属于难题.


科目:高中数学 来源: 题型:选择题
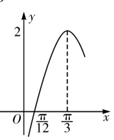 函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )
函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )| A. | [-$\sqrt{2}$,2] | B. | (-1,$\sqrt{2}$] | C. | [0,2] | D. | [-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-1 | B. | $\sqrt{5}$+1 | C. | 2$\sqrt{5}$+2 | D. | 2$\sqrt{5}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com