
���� ������������������ʽ���ϵ�����ɵõ����ۣ�
������������ʽ���Ӧ��ƽ�������������Թ滮�Ľ��н���ƽ��Ŀ�꺯�����������ν�Ͻ�����⼴�ɣ�
��� 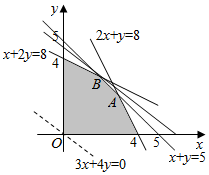 �⣺������֪���ݣ��б�����
�⣺������֪���ݣ��б�����
ԭ�ϣ��֣�ԭ�ϣ��֣�ԭ�ϣ��֣�ÿ�ּײ�Ʒ112ÿ���Ҳ�Ʒ121ԭ����588
| Aԭ�ϣ��֣� | Bԭ�ϣ��֣� | Cԭ�ϣ��֣� | |
| ÿ�ּײ�Ʒ | 1 | 1 | 2 |
| ÿ���Ҳ�Ʒ | 1 | 2 | 1 |
| ԭ���� | 5 | 8 | 8 |
���� ������Ҫ�������Թ滮��Ӧ�����⣬����������������ʽ���ϵ���������ν���ǽ������Ĺؼ�������ѧ�����������ͼ������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$ | B�� | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n}}$+����2 | ||
| C�� | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n}}$=1 | D�� | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n}}$��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [e+1��+�ޣ� | B�� | ��e+1��+�ޣ� | C�� | ��e-1��+�ޣ� | D�� | [e-1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3$\sqrt{6}$ | B�� | 4$\sqrt{6}$ | C�� | 6$\sqrt{6}$ | D�� | 12$\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com