练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．甲、乙、丙三种溶液分别重147g、343g、133g，现要将它们分别全部装入小瓶中，若小瓶装入液体的质量相同，则每瓶最多装7g．

    分析 由已知可得每瓶最多装的质量，即为147、343、133的最大公约数，进而得到答案．

    解答 解：由已知可得每瓶最多装的质量，即为147、343、133的最大公约数，
    ∵147=133+14，
    133=14×9+7，
    14=7×2，
    343=7×49，
    故147、343、133的最大公约数为7，
    故每瓶最多装7g．
    故答案为：7．

    点评 本题考查的知识点是最大公约数，熟练掌握辗转相除法求最大公约数的方法和步骤是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．用数字1，2，3和减号“-”组成算式进行运算，要求每个算式中包含所有数字，且每个数字和减号“-”只能用一次，则不同的运算结果的种数为（　　）
    A．6B．8C．10D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某企业生产甲、乙两种产品均需用A、B、C三种原料．已知生产1吨甲产品需A原料1吨，B原料1吨，C原料2吨；生产1吨乙产品需A原料1吨，B原料2吨，C原料1吨；每天可供使用的A原料不超过5吨，B原料和C原料均不超过8吨．
    （Ⅰ） 若生产1吨甲、乙产品可获利润分别为3万元、4万元，每天生产x吨甲产品和y吨乙产品共可获得利润z万元，请列出满足上述条件的不等式组及目标函数；
    （Ⅱ） 在（Ⅰ）的条件下，求该企业每天可获得的最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知集合A={y|y=x+$\sqrt{x}$}，B={-3，-1，2，4}，则A∩B中元素的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

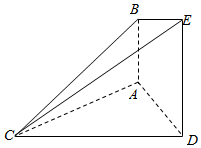    12．如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB．
    （1）求证：平面BCE⊥平面CDE；
    （2）若AB=1，求四棱锥C-ABED的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知A（2，0），P是圆C：x2+y2+4x-32=0上的动点，线段AP的垂直平分线与直线PC的交点为M，则当P运动时．点M的轨迹方程是$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．容器C的内、外壁分别为棱长为2a和2a+2的正方体，容器S的内、外壁分别为半径为r和r+1的球形，若两个容器的容积相同，则关于两个容器的体积VC和VS，下列说法正确的是（　　）
    A．存在满足条件的a，r，使得VC＜VS
    B．对任意满足条件的a，r，使得VC=VS
    C．对任意满足条件的a，r，使得VC＞VS
    D．存在唯一一组条件的a，r，使得VC=VS

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知实数x，y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{4x-y-4≤0}}\end{array}\right.$，则当3x-y取得最小值时，$\frac{x-5}{y+3}$的值为-$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下面随机变量X的分布列不属于二项分布的是（　　）
    A．据中央电视台新闻联播报道，一周内在某网站下载一次数据，电脑被感染某种病毒的概率是0.65，设在这一周内，某电脑从该网站下载数据n次中被感染这种病毒的次数为X
    B．某射手射击击中目标的概率为p，设每次射击是相互独立的，从开始射击到击中目标所需要的射击次数为X
    C．某射手射击击中目标的概率为p，设每次射击是相互独立的，射击n次命中目标的次数为X
    D．位于某汽车站附近有一个加油站，汽车每次出站后到这个加油站加油的概率为0.6，国庆节这一天有50辆汽车开出该站，假设一天里汽车去该加油站加油是相互独立的，去该加油站加油的汽车数为X

    查看答案和解析>>

    同步练习册答案