练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝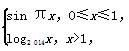

    若a，b，c互不相等，且f(a)＝f(b)＝f(c)，则a＋b＋c的取值范围是(　　)

    A．(1,2 014)                            B．(1,2 015) 

    C．(2,2 015)                            D．[2,2 015]


    C

    [解析]　函数f(x)＝的图象如图所示，不妨令a<b<c，

    由正弦曲线的对称性可知，a＋b＝1，而1<c<2 014.所以2<a＋b＋c<2 015，故选C.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(　　)

    A．α与β相交，且交线平行于l   

    B．α与β相交，且交线垂直于l

    C．α∥β，且l∥α   

    D．α⊥β，且l⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝2x2＋px＋q，g(x)＝x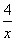＋是定义在集合M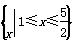＝上的两个函数．对任意的x∈M，存在常数x0∈M，使得f(x)≥f(x0)，g(x)≥g(x0)，且f(x0)＝g(x0)．则函数f(x)在集合M上的最大值为(　　)

    A.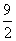                                    B．4 

    C．6                                    D.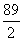

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(n)＝logn＋1(n＋2)(n∈N*)，定义使f(1)·f(2)·f(3)·…·f(k)为整数的数k(k∈N*)叫做企盼数，则在区间[1,2 013]内这样的企盼数共有________个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)的图象向右平移a(a>0)个单位后关于x＝a＋1对称，当x2>x1>1时，[f(x2)－f(x1)](x2－x1)<0恒成立，设a＝f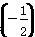，b＝f(2)，c＝f(e)，则a，b，c的大小关系为(　　)

    A．c>a>b                                B．c>b>a 

    C．a>c>b                                D．b>a>c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知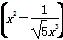5的展开式中的常数项为T，f(x)是以T为周期的偶函数，且当x∈[0,1]时，f(x)＝x，若在区间[－1,3]内，函数g(x)＝f(x)－kx－k有4个零点，则实数k的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)是偶函数，当x∈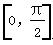时，f(x)＝xsin x，若a＝f(cos 1)，b＝f(cos 2)，c＝f(cos 3)，则a，b，c的大小关系为(　　)

    A．a<b<c                                B．b<a<c 

    C．c<b<a                                D．b<c<a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在满足不等式组的平面点集中随机取一点M(x0，y0)，设事件A＝“y0<2x0”，那么事件A发生的概率是(　　)

    A.  B.  C.  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出如下四个叙述：

    ①若“p且q”为假命题，则p，q均为假命题；

    ②命题“若a>b，则2a>2b－1”的否命题为“若a≤b，则2a≤2b－1”；

    ③“∀x∈R，x2＋1≥1”的否定是“∃x∈R，x2＋1≤1”；

    ④在△ABC中，“A>B”是“sin A>sin B”的充要条件．

    其中叙述不正确的个数是(　　)

    A．4  B．3  C．2  D．1

    查看答案和解析>>

    同步练习册答案